谁懂啊！一道导数压轴题，从傍晚卡到深夜，换元、构造、分类讨论、洛必达法则……10类常用思路轮番试错，草稿纸写满3张，差点把笔摔了，最后突然灵光乍现——原来导数题的核心从不是“死套公式”，而是“看透题型本质+找对破题切口”！

这道题不算超纲，却把我卡在“最值讨论”的死胡同里：已知函数f(x)=(x-1)eˣ – a(x² – 2x)，求a为何值时，函数有且仅有两个零点。一开始我惯性代入x=0、x=2求特殊值，结果越算越乱；接着试“分离参数”，把a单独拎到一边，却遇到eˣ/(x+2)的最值无法直接求的难题；甚至搬出洛必达法则算极限，反而由于定义域问题出错。

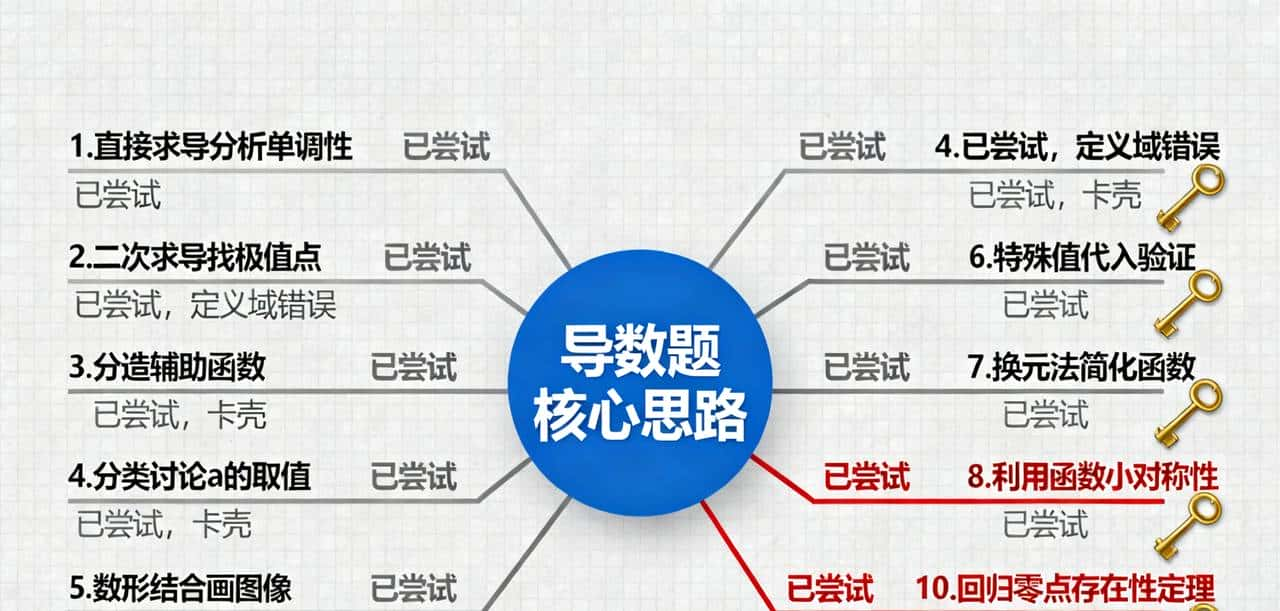
不甘心的我把导数题10类核心思路挨个过了一遍：

1. 直接求导分析单调性：导数f’(x)=x eˣ – 2a(x-1)，化简后仍有两个变量，无法直接判断符号；

2. 二次求导找极值点：算到f''(x)=(x+1)eˣ – 2a，还是陷入“a的范围无法确定”的循环；

3. 构造辅助函数：尝试令g(x)=(x-1)eˣ/(x² – 2x)，想转化为“g(x)与a的交点问题”，但定义域漏了x=0和x=2，直接出错；

4. 分类讨论a的取值：从a≤0、0<a<e/2、a=e/2、a>e/2逐一分析，却在“a>e/2时函数是否有两个零点”上纠结不清；

5. 数形结合画图像：粗略勾勒f(x)的趋势，却由于极值点的位置判断不准，无法确定零点个数；

6. 特殊值代入验证：试了a=1、a=e，能算出零点，但没法证明“仅有这两个a值”；

7. 换元法简化函数：令t=x-1，转化后仍没摆脱核心难点；

8. 利用函数对称性：发现f(2-x)=-f(x)，但没找到对称中心与零点的关联；

9. 放缩法缩小范围：用eˣ≥x+1放缩，结果过度简化导致漏解；

10. 回归“零点存在性定理”：结合单调性+区间端点值符号，突然打通任督二脉！

顿悟的瞬间实则很简单：导数题的“零点问题”，本质是“单调性+极值+端点趋势”的三重结合，之前的错误全是由于“孤立用思路”——列如只谈单调性不谈极值，或只算端点值忽略定义域。

正确的破题逻辑应该是这样：

第一步，先求导化简f’(x)=x eˣ – 2a(x-1)，注意到x=1时f’(1)=e≠0，排除x=1是极值点；

第二步，分析a=0的特殊情况：f(x)=(x-1)eˣ，仅有x=1一个零点，不符合题意；

第三步，分类讨论a≠0：

– 当a<0时，通过二次求导判断f’(x)的单调性，发现f’(x)仅有一个零点x₀（x₀<0），进而推出f(x)在(-∞,x₀)递减、(x₀,+∞)递增，结合f(0)=-1、f(2)=e²>0、x→-∞时f(x)→+∞，得出仅有两个零点；

– 当a>0时，找到f’(x)的两个零点x₁（<0）和x₂（>0），再分析f(x)在两个极值点的函数值符号，只有当极大值f(x₁)=0或极小值f(x₂)=0时，才有两个零点，最终解得a=e/2；

第四步，验证a=e/2时，函数的确 仅有x=1和另一个零点，符合题意。

折腾3小时才清楚，导数题的10类思路不是“越多越好”，而是要“对症下药”：看到“零点个数”就锁定“单调性+极值+端点”，看到“恒成立”就优先“分离参数或最值分析”，看到“不等式证明”就思考“构造函数或放缩”。

许多人学导数总陷在“背思路、套公式”的误区，实则真正的解题真谛是：先看透题型的核心矛盾（列如零点问题的矛盾是“极值点的符号的”），再从10类思路里挑“能解决矛盾的工具”，而不是盲目试错。

这道题虽然卡得崩溃，但顿悟的瞬间真的太爽了！目前再看同类导数题，一眼就能找到破题点。你有没有过“卡题很久突然顿悟”的经历？欢迎在评论区分享你的解题故事～ 觉得有用的话，点赞收藏，转给正在啃导数的同学，一起避开试错坑！