泰坦尼克号乘客生存预测

泰坦尼克号是英国白星航运公司旗下的一艘奥林匹克级邮轮，被誉为“永不沉没”的巨轮。它于1909年3月31日动工建造，1911年5月31日下水，1912年4月2日完工试航。泰坦尼克号排水量达46000吨，全长269.06米，宽28.19米，是当时世界上体积最庞大、内部设施最豪华的客运轮船。1912年4月10日，泰坦尼克号从英国南安普敦港出发，前往美国纽约，进行其处女航。船上搭载了2224名船员及乘客，包括许多富有和知名的乘客。
1912年4月14日23时40分左右，泰坦尼克号在北大西洋航行时，与一座冰山相撞。撞击导致船体右舷出现裂缝，海水迅速涌入船内。尽管泰坦尼克号设计有16个水密舱，但撞击导致其中5个舱室进水，超过了船只设计的承受能力。随着海水的不断涌入，船体逐渐失去平衡，最终在4月15日凌晨2时20分左右断裂成两截，沉入大西洋底3700米处。该事件成为了20世纪最著名的海难之一，共造成了1517人丧生。
著名的机器学习竞赛网站Kaggle的第一个教学例子就是泰坦尼克号乘客生存预测。这次我们也用kaggle提供的数据来做一个泰坦尼克号乘客的生存情况预测。
kagggle提供了一个train.csv和test.csv。在train.csv中提供了891名乘客的信息，以及他们是遇难还是生还的信息。在test.csv中提供了418名乘客的信息，比赛就是用train.csv训练出来的模型来预测这418名乘客是遇难还是生还，根据预测来正确率来评分。
泰坦尼克号乘客的生存概率预测本质上是一个二分类问题，根据训练数据的特征值来学习出一个模型。我们第一要对数据进行一些处理，train.csv中的字段含义如下：

import pandas as pd
import numpy as np

df = pd.read_csv( train.csv )
df_predict = pd.read_csv( test.csv )

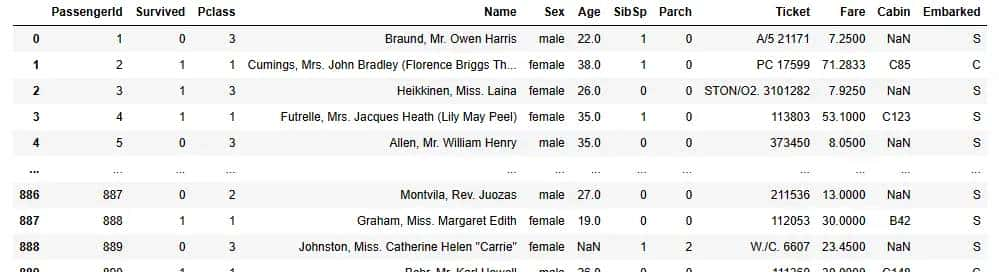
第一数据进行缺失值的处理，由于训练数据中有些字段是空的，我们需要预先填充好。

# 缺失值处理
# 年龄用中位数填充
df[ Age ].fillna(df[ Age ].median(), inplace=True)
# 票价用中位数填充
df[ Fare ].fillna(df[ Fare ].median(), inplace=True)
# 登船港口用众数填充
df[ Embarked ].fillna(df[ Embarked ].mode()[0], inplace=True)
# 客舱缺失值标记为 Unknown 
df[ Cabin ].fillna( Unknown , inplace=True)

然后对类别字段进行数值化表明（决策树等模型可以直接使用文本格式的属性进行学习，但是逻辑回归等模型不行，所以还是统一进行了数值化处理）。

# 性别数值化，女性为1，男性为0
df[ Sex ] = df[ Sex ].map({ female : 1,  male : 0})

# 计算家庭大小
df[ FamilySize ] = df[ SibSp ] + df[ Parch ] + 1

# 定义家庭类别
def get_family_category(family_size):
    if family_size == 1:
        return 0  # 小家庭
    elif 2 <= family_size <= 4:
        return 1  # 中等家庭
    else:
        return 2  # 大家庭

df[ FamilyCategory ] = df[ FamilySize ].apply(get_family_category)

对一些类别型的字段，也可以采用One-hot方式来表明。

# 对登船港口做one-hot
df = pd.get_dummies(df, columns=[ Embarked ], drop_first=True)
# 把乘客分成Miss,Mrs,Mr,Master四个称谓，并做one-hot处理
df[ Title ] = df[ Name ].str.extract(  ([A-Za-z]+). , expand=False)
df[ Title ] = df[ Title ].replace([ Dr ,  Rev ,  Col ,  Major ,  Ms ,  Lady ,  Sir ,  Jonkheer ,  Don ,  Dona ,  Mme ,  Capt ,  the Countess ],  Rare )
df[ Title ] = df[ Title ].replace( Mlle ,  Miss ).replace( Ms ,  Miss ).replace( Mrs ,  Mrs ).replace( Mr ,  Mr ).replace( Miss ,  Miss )
df = pd.get_dummies(df, columns=[ Title ], drop_first=True)

接下来就可以进行训练了。二分类最简单的模型就是逻辑回归，我先用逻辑回归来训练一下这个数据集。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns


def train_model(df):
    """训练逻辑回归模型"""
    # 分割特征和目标变量
    # 选择相关特征
    # features = [ Pclass ,  Sex ,  Age ,  Fare ,  FamilyCategory ,  Embarked_Q ,  Embarked_S ]
    features = [ Pclass ,  Sex ,  Age ,  Fare ,  FamilyCategory ,  Embarked_Q ,  Embarked_S ,  Title_Master ,  Title_Miss ,  Title_Mr ,  Title_Mrs ,  Title_Rare ]
    X = df[features]
    #y = df[ Survived ]
    #X = df.drop( Survived , axis=1)
    y = df[ Survived ]
    
    # 特征标准化
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X)
    
    # 划分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42, stratify=y)
    
    # 训练逻辑回归模型
    model = LogisticRegression(max_iter=1000, random_state=42)
    model.fit(X_train, y_train)
    
    # 在测试集上预测
    y_pred = model.predict(X_test)
    
    # 模型评估
    accuracy = accuracy_score(y_test, y_pred)
    cm = confusion_matrix(y_test, y_pred)
    report = classification_report(y_test, y_pred)
    print(f"
模型准确率: {accuracy:.4f}")
    print("
分类报告:")
    print(report)
    return model, scaler, X.columns


def predict_model(model, df_predict):
    """测试逻辑回归模型"""
    # 特征标准化
    scaler = StandardScaler()
    X_predict = scaler.fit_transform(df_predict)
    y_pred = model.predict(X_predict)
    print("y_pred:", y_pred)
    
model, scaler, columns = train_model(df)
# 输出
模型准确率: 0.8268

分类报告:
              precision    recall  f1-score   support

           0       0.84      0.88      0.86       110
           1       0.80      0.74      0.77        69

    accuracy                           0.83       179
   macro avg       0.82      0.81      0.81       179
weighted avg       0.83      0.83      0.83       179

可以看到，训练精度达到了0.82。
下面我们改成用决策树，代码几乎不用改，只要将使用的模型改成决策树模型即可：

# 在测试集上预测
model = DecisionTreeClassifier(random_state=42)
model.fit(X_train, y_train)

得到的精度也是0.82，超级接近逻辑回归。
接下来，我们改用神经网络感知机试试，用pytorch实现。用pytorch做训练，就要先把数据格式转成tensor，并封装成Dataset和Dataloader。

X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)

# 转换为PyTorch张量
X_train_tensor = torch.FloatTensor(X_train)
y_train_tensor = torch.FloatTensor(y_train).view(-1, 1)  # 调整形状为二维张量
X_val_tensor = torch.FloatTensor(X_val)
y_val_tensor = torch.FloatTensor(y_val).view(-1, 1)

# 创建数据加载器
batch_size = 32
train_dataset = TensorDataset(X_train_tensor, y_train_tensor)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_dataset = TensorDataset(X_val_tensor, y_val_tensor)
val_loader = DataLoader(val_dataset, batch_size=batch_size)

定义一个简单的多层感知机，算是一个最简单的深度学习模型。

class TitanicMLP(nn.Module):
    def __init__(self, input_size):
        super(TitanicMLP, self).__init__()
        self.layer1 = nn.Linear(input_size, 64)
        self.layer2 = nn.Linear(64, 32)
        self.layer3 = nn.Linear(32, 16)
        self.output = nn.Linear(16, 1)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()
        self.dropout = nn.Dropout(0.3)  # 防止过拟合
        
    def forward(self, x):
        x = self.relu(self.layer1(x))
        x = self.dropout(x)
        x = self.relu(self.layer2(x))
        x = self.dropout(x)
        x = self.relu(self.layer3(x))
        x = self.dropout(x)
        x = self.sigmoid(self.output(x))  # 二分类
        return x

训练模型:

# 初始化模型
input_size = X_train.shape[1]
model = TitanicMLP(input_size)

epochs = 200
train_losses = []
val_losses = []
best_val_loss = float( inf )
early_stopping_patience = 10
counter = 0
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.Adam(model.parameters(), lr=0.001)

for epoch in range(epochs):
    # 训练阶段
    model.train()
    train_loss = 0
    for batch_X, batch_y in train_loader:
        # 前向传播
        outputs = model(batch_X)
        loss = criterion(outputs, batch_y)
        # 反向传播和优化
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        train_loss += loss.item()
    
    # 验证阶段
    model.eval()
    val_loss = 0
    val_preds = []
    val_labels = []
    with torch.no_grad():
        for batch_X, batch_y in val_loader:
            outputs = model(batch_X)
            loss = criterion(outputs, batch_y)
            val_loss += loss.item()
            # 保存预测结果用于评估
            val_preds.extend(outputs.numpy())
            val_labels.extend(batch_y.numpy())
    
    # 计算平均损失
    train_loss /= len(train_loader)
    val_loss /= len(val_loader)
    train_losses.append(train_loss)
    val_losses.append(val_loss)
    
    # 计算验证集准确率和AUC
    val_preds_binary = (np.array(val_preds) > 0.5).astype(int)
    val_accuracy = accuracy_score(val_labels, val_preds_binary)
    val_auc = roc_auc_score(val_labels, val_preds)
    
    # 打印训练进度
    if (epoch + 1) % 10 == 0:
        print(f Epoch [{epoch+1}/{epochs}], Train Loss: {train_loss:.4f}, Val Loss: {val_loss:.4f}, Val Acc: {val_accuracy:.4f}, Val AUC: {val_auc:.4f} )
        
# 绘制训练和验证损失曲线
plt.figure(figsize=(10, 6))
plt.plot(train_losses, label= Training Loss )
plt.plot(val_losses, label= Validation Loss )
plt.title( Training and Validation Loss )
plt.xlabel( Epoch )
plt.ylabel( Loss )
plt.legend()
plt.show()

Epoch [10/200], Train Loss: 0.6001, Val Loss: 0.6088, Val Acc: 0.6536, Val AUC: 0.6896
Epoch [20/200], Train Loss: 0.5705, Val Loss: 0.5760, Val Acc: 0.6648, Val AUC: 0.7270
Epoch [30/200], Train Loss: 0.5279, Val Loss: 0.5370, Val Acc: 0.7318, Val AUC: 0.7762
Epoch [40/200], Train Loss: 0.5098, Val Loss: 0.4932, Val Acc: 0.7821, Val AUC: 0.8203
Epoch [50/200], Train Loss: 0.4912, Val Loss: 0.4626, Val Acc: 0.7989, Val AUC: 0.8343
Epoch [60/200], Train Loss: 0.4613, Val Loss: 0.4558, Val Acc: 0.7877, Val AUC: 0.8390
Epoch [70/200], Train Loss: 0.4594, Val Loss: 0.4469, Val Acc: 0.8101, Val AUC: 0.8415
Epoch [80/200], Train Loss: 0.4536, Val Loss: 0.4372, Val Acc: 0.8212, Val AUC: 0.8484
Epoch [90/200], Train Loss: 0.4514, Val Loss: 0.4362, Val Acc: 0.8212, Val AUC: 0.8497
Epoch [100/200], Train Loss: 0.4494, Val Loss: 0.4237, Val Acc: 0.8212, Val AUC: 0.8576
Epoch [110/200], Train Loss: 0.4232, Val Loss: 0.4211, Val Acc: 0.8268, Val AUC: 0.8631
Epoch [120/200], Train Loss: 0.4055, Val Loss: 0.4243, Val Acc: 0.8268, Val AUC: 0.8609
Epoch [130/200], Train Loss: 0.4139, Val Loss: 0.4214, Val Acc: 0.8212, Val AUC: 0.8640
Epoch [140/200], Train Loss: 0.4181, Val Loss: 0.4242, Val Acc: 0.8101, Val AUC: 0.8631
Epoch [150/200], Train Loss: 0.4162, Val Loss: 0.4200, Val Acc: 0.8212, Val AUC: 0.8671
Epoch [160/200], Train Loss: 0.3999, Val Loss: 0.4244, Val Acc: 0.8101, Val AUC: 0.8646
Epoch [170/200], Train Loss: 0.3950, Val Loss: 0.4083, Val Acc: 0.8324, Val AUC: 0.8714
Epoch [180/200], Train Loss: 0.4063, Val Loss: 0.4097, Val Acc: 0.8380, Val AUC: 0.8719
Epoch [190/200], Train Loss: 0.4060, Val Loss: 0.4105, Val Acc: 0.8492, Val AUC: 0.8723
Epoch [200/200], Train Loss: 0.3798, Val Loss: 0.4179, Val Acc: 0.8212, Val AUC: 0.8694

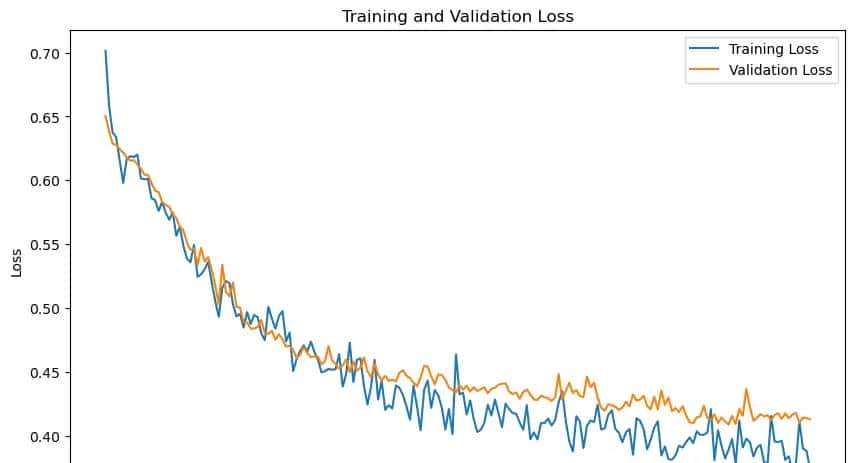
可以看到，训练精度在0.83~0.84左右，比之前两个模型稍好。
最后，我们来看看使用模型集成方法，进行投票后精度可以达到多少。
先使用几个通用模型来单独训练，并评估精度。

from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score, StratifiedKFold
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.ensemble import (RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier, 
                              VotingClassifier, StackingClassifier)
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix

# 定义基础模型
models = {
     Logistic Regression : LogisticRegression(random_state=42),
     Random Forest : RandomForestClassifier(random_state=42),
     Gradient Boosting : GradientBoostingClassifier(random_state=42),
     SVM : SVC(random_state=42, probability=True),
     KNN : KNeighborsClassifier()
}

# 训练并评估每个模型
results = {}
for name, model in models.items():

    # 交叉验证
    cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
    scores = cross_val_score(model, X_train, y_train, cv=cv, scoring= accuracy )

    # 训练模型
    model.fit(X_train, y_train)
    
    # 测试集评估
    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    
    results[name] = {
         cv_mean : scores.mean(),
         cv_std : scores.std(),
         test_accuracy : accuracy
    }
    
    print(f"{name}: CV accuracy = {scores.mean():.4f} ± {scores.std():.4f}, Test accuracy = {accuracy:.4f}")
# 输出
Logistic Regression: CV accuracy = 0.8203 ± 0.0227, Test accuracy = 0.8436
Random Forest: CV accuracy = 0.8034 ± 0.0154, Test accuracy = 0.8101
Gradient Boosting: CV accuracy = 0.8174 ± 0.0346, Test accuracy = 0.7933
SVM: CV accuracy = 0.6854 ± 0.0217, Test accuracy = 0.6201
KNN: CV accuracy = 0.7248 ± 0.0297, Test accuracy = 0.6816

从泰坦尼克号数据集来看，逻辑回归的精度最好，随机森林和梯度集成效果也还可以，K近邻和支持向量机精度较差。

# 定义软投票集成模型
soft_voting_clf = VotingClassifier(
    estimators=[
        ( lr , LogisticRegression(random_state=42)),
        ( rf , RandomForestClassifier(random_state=42)),
        ( Gradient Boosting , GradientBoostingClassifier(random_state=42))
    ],
    voting= soft   # 概率平均
)
soft_voting_clf.fit(X_train, y_train)
# 评估
y_pred_soft_voting = soft_voting_clf.predict(X_test)
print(f"软投票集成准确率: {accuracy_score(y_test, y_pred_soft_voting):.4f}")
# 输出
软投票集成准确率: 0.8547

# 定义投票集成模型
voting_clf = VotingClassifier(
    estimators=[
        ( lr , LogisticRegression(random_state=42)),
        ( rf , RandomForestClassifier(random_state=42)),
        ( Gradient Boosting , GradientBoostingClassifier(random_state=42))
    ],
    voting= hard   # 多数表决
)
voting_clf.fit(X_train, y_train)
# 评估
y_pred_voting = voting_clf.predict(X_test)
print(f"硬投票集成准确率: {accuracy_score(y_test, y_pred_voting):.4f}")
# 输出
硬投票集成准确率: 0.8380

# 定义基础模型和元模型
estimators = [
    ( lr , LogisticRegression(random_state=42)),
    ( rf , RandomForestClassifier(random_state=42)),
    ( Gradient Boosting , GradientBoostingClassifier(random_state=42))
]

stacking_clf = StackingClassifier(
    estimators=estimators,
    final_estimator=LogisticRegression(random_state=42)  # 元模型
)

stacking_clf.fit(X_train, y_train)

# 评估
y_pred_stacking = stacking_clf.predict(X_test)
print(f"堆叠集成准确率: {accuracy_score(y_test, y_pred_stacking):.4f}")
# 输出
堆叠集成准确率: 0.8492

这里有个很有意思的地方，如果我把GradientBoosting方法换成SVM，精度可以达到0.8659，这是目前最高的精度，可能SVM在这个数据集上单独训练精度不高，但是用堆叠方式进行集成精度提升反而最大。
可以看到，集成方法的精度的确 要比单个方法的精度更高，这里神经网络或者说深度学习的精度并没有太高主要是这个案例数据量的确 比较小，如果换到一个数据量足够多的情况下，随着神经网络层数的加深以及训练轮次的增多，深度学习的精度往往会超越传统机器学习方法。