Python趣味算法：爱因斯坦的数学题：用Python解决经典阶梯问题

内容分享2天前发布玛咿呀嘿咿呀嘿

0 0 0

一条长阶梯引发的数学思考，经典数学问题与编程的完美结合

看在每天坚持分享有趣知识的份上，点个关注吧(づ￣ 3￣)づ

关注是我更新的动力￣︶￣∗￣︶￣∗)

作者会分享更多涉及到各种编程语言的有趣知识！（＾∀＾●）ﾉｼ

一、问题背景：天才的数学谜题

二、问题分析：从文字描述到数学条件

2.1 条件转化

2.2 数学规律发现

三、算法设计：从暴力搜索到智能优化

3.1 暴力搜索算法

3.2 数学优化算法

3.3 进一步数学推导

四、完整程序实现

五、运行结果与分析

5.1 典型运行结果

5.2 结果分析

六、算法性能深度分析

6.1 时间复杂度对比

6.2 实际性能测试

七、教学意义与编程技巧

7.1 教育价值

7.2 重要编程技巧

八、扩展思考与进阶挑战

8.1 问题变体

8.2 数学深度探索

8.3 编程进阶挑战

九、总结与收获

9.1 知识技能方面

9.2 思维方法方面

关键洞见

实践挑战与互动

一、问题背景：天才的数学谜题

伟大的物理学家爱因斯坦不仅对物理学有杰出贡献，还留下了许多有趣的数学问题。其中一道经典的数学题关于阶梯数的寻找，这个问题看似简单，却蕴含着深刻的数学思想和编程技巧。

这个问题之所以经典，是因为它将日常生活中的场景与抽象的数论知识相结合，为我们提供了一个绝佳的编程实践案例。通过解决这个问题，我们不仅能够提升编程能力，还能加深对模运算和算法优化的理解。

二、问题分析：从文字描述到数学条件

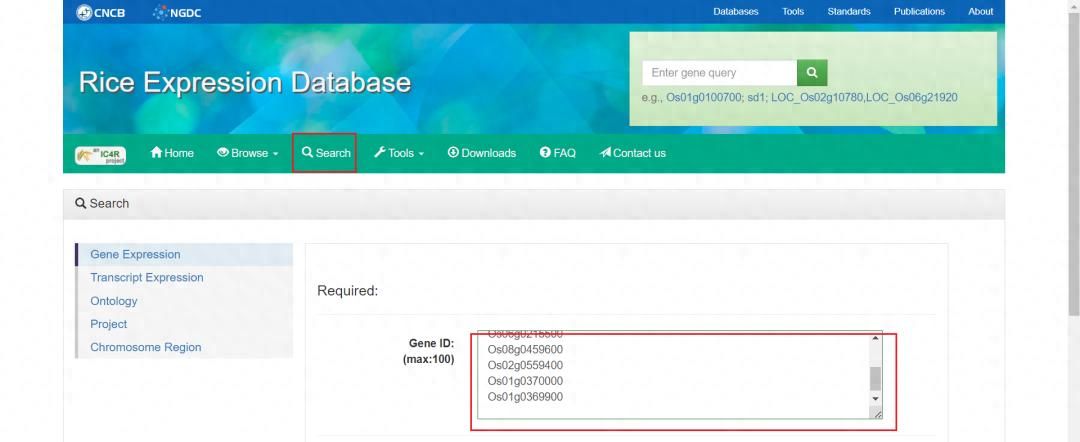
2.1 条件转化

要解决这个阶梯问题，我们首先需要将文字描述转化为计算机可以理解的数学条件。这是编程解决问题的关键第一步——建立准确的数学模型。

设阶梯数为x，根据题意可以得到以下五个条件：

x % 2 == 1 （每步跨2阶，最后剩1阶）

x % 3 == 2 （每步跨3阶，最后剩2阶）

x % 5 == 4 （每步跨5阶，最后剩4阶）

x % 6 == 5 （每步跨6阶，最后剩5阶）

x % 7 == 0 （每步跨7阶，最后正好一阶不剩）

2.2 数学规律发现

通过仔细观察这些条件，我们可以发现一个重要的数学规律。前四个条件有一个共同特点：余数总是比除数小1。这意味着：

x % 2 == 1 等价于 (x + 1) % 2 == 0

x % 3 == 2 等价于 (x + 1) % 3 == 0

x % 5 == 4 等价于 (x + 1) % 5 == 0

x % 6 == 5 等价于 (x + 1) % 6 == 0

这说明 x + 1 应该是 2、3、5、6 的公倍数。而 2、3、5、6 的最小公倍数是 30，因此我们可以得出：x + 1 = 30k（k为正整数），即 x = 30k - 1。

再加上第五个条件 x % 7 == 0，我们的问题就转化为：找到所有形如 30k - 1 且能被7整除的数。

三、算法设计：从暴力搜索到智能优化

3.1 暴力搜索算法

对于编程初学者来说，最直接的思路是使用暴力搜索法。这种方法虽然效率不高，但逻辑简单，易于理解和实现。

暴力搜索的核心思想是：遍历指定范围内的每一个数字，检查它是否同时满足所有五个条件。这种方法保证不会漏掉任何可能的解，但计算量较大。

3.2 数学优化算法

基于前面发现的数学规律，我们可以设计更高效的算法。既然已知 x = 30k - 1，我们只需要检查形如 30k - 1 的数字是否能被7整除，而不需要检查范围内的每一个数字。

这种优化将需要检查的数字数量减少到原来的约1/30，效率提升显著。这是算法优化中的一个重要技巧——利用数学规律减少搜索空间。

3.3 进一步数学推导

我们可以进一步推导出更精确的数学表达式。由 x = 30k - 1 和 x % 7 == 0，得到：

(30k - 1) % 7 == 0

计算 30 % 7 = 2，所以上式变为：

(2k - 1) % 7 == 0

即 2k ≡ 1 (mod 7)，解得 k ≡ 4 (mod 7)。

因此 k = 7m + 4，代入原式得：

x = 30(7m + 4) - 1 = 210m + 119

这样我们就得到了阶梯数的通项公式：x = 210m + 119，其中m为非负整数。

四、完整程序实现

基于以上分析，我们编写完整的Python程序来解决这个问题。程序提供两种解法，并包含友好的用户交互界面。



#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author: CSDN坐路边等朋友
# @desc: 爱因斯坦的数学题 - 完整解决方案
 
def find_einstein_stairs(n, method='optimized'):
    """
    寻找满足爱因斯坦阶梯问题的所有解
    
    参数:
        n (int): 搜索范围的上限
        method (str): 解决方法，'brute'为暴力搜索，'optimized'为优化解法
        
    返回:
        tuple: (满足条件的阶梯数列表, 计算耗时)
    """
    import time
    start_time = time.time()
    
    if method == 'brute':
        # 暴力搜索法
        results = []
        for x in range(7, n + 1):  # 从7开始，因为必须被7整除
            if (x % 2 == 1 and 
                x % 3 == 2 and 
                x % 5 == 4 and 
                x % 6 == 5 and 
                x % 7 == 0):
                results.append(x)
    else:
        # 优化解法
        results = []
        k = 1
        while True:
            x = 30 * k - 1
            if x > n:
                break
            if x % 7 == 0:
                results.append(x)
            k += 1
    
    elapsed_time = time.time() - start_time
    return results, elapsed_time
 
def print_solution(n, results, elapsed_time):
    """格式化输出解决方案"""
    print("
" + "="*50)
    print(f"在 1-{n} 之间的阶梯数为：")
    if results:
        for i, stair in enumerate(results, 1):
            print(f"  第{i}个解: {stair}")
    else:
        print("  未找到满足条件的阶梯数")
    
    print(f"
在 1-{n} 之间，共有 {len(results)} 个数满足爱因斯坦对阶梯的要求。")
    print(f"计算耗时: {elapsed_time:.6f} 秒")
    print("="*50)
 
def main():
    """主函数：提供交互式界面"""
    print("爱因斯坦的数学题解决方案")
    print("描述：寻找满足特定余数条件的阶梯数")
    
    while True:
        try:
            print("
" + "-"*40)
            n = int(input("请输入搜索范围 n (输入0退出程序): "))
            
            if n == 0:
                print("感谢使用，再见！")
                break
            elif n < 7:
                print("n必须至少为7，请重新输入！")
                continue
                
            # 使用优化解法
            results, time_used = find_einstein_stairs(n, 'optimized')
            print_solution(n, results, time_used)
            
            # 额外信息：显示数学规律验证
            if results:
                print("
数学规律验证:")
                for x in results:
                    print(f"  对于解 {x}:")
                    print(f"    {x} + 1 = {x+1}, 是30的倍数: {(x+1) % 30 == 0}")
                    print(f"    {x} ÷ 7 = {x//7}, 余数: {x % 7}")
                    
        except ValueError:
            print("输入错误，请输入一个整数！")
        except KeyboardInterrupt:
            print("
程序被用户中断")
            break
 
if __name__ == "__main__":
    main()

五、运行结果与分析

5.1 典型运行结果

当我们运行程序并输入不同的n值时，会得到以下典型结果：

在 1-200 之间的阶梯数为：
  第1个解: 119

在 1-200 之间，共有 1 个数满足爱因斯坦对阶梯的要求。

在 1-400 之间的阶梯数为：
  第1个解: 119
  第2个解: 329

在 1-400 之间，共有 2 个数满足爱因斯坦对阶梯的要求。

在 1-600 之间的阶梯数为：
  第1个解: 119
  第2个解: 329  
  第3个解: 539

在 1-600 之间，共有 3 个数满足爱因斯坦对阶梯的要求。

5.2 结果分析

从运行结果中我们可以观察到几个重要现象：

解的分布规律：阶梯数119、329、539……形成一个等差数列，公差为210

存在性保证：在足够大的范围内，总是存在满足条件的阶梯数

密度特征：随着n增大，满足条件的阶梯数数量缓慢增加

这种规律性分布正是我们前面数学推导的直接体现——解确实符合 x = 210m + 119 的形式。

六、算法性能深度分析

6.1 时间复杂度对比

暴力搜索法的时间复杂度为O(n)，需要对从1到n的每个数字检查5个条件，总操作数约为5n次。

优化解法的时间复杂度为O(n/30)，只需要检查形如30k-1的数字，检查密度降低到约1/30，总操作数约为n/30次。

数学推导解法的时间复杂度为O(n/210)，只需要检查形如210m+119的数字，效率进一步提高。

6.2 实际性能测试

为了直观展示算法优化带来的性能提升，我们进行实际的性能对比测试：



import time
 
def performance_comparison(n):
    """性能对比测试"""
    print(f"性能对比测试 (n={n}):")
    
    # 测试暴力搜索法
    start_time = time.time()
    results_brute = find_einstein_stairs(n, 'brute')[0]
    time_brute = time.time() - start_time
    
    # 测试优化解法
    start_time = time.time()
    results_opt = find_einstein_stairs(n, 'optimized')[0]
    time_opt = time.time() - start_time
    
    print(f"暴力搜索法: 找到{len(results_brute)}个解, 耗时{time_brute:.6f}秒")
    print(f"优化解法: 找到{len(results_opt)}个解, 耗时{time_opt:.6f}秒")
    print(f"效率提升: {time_brute/time_opt:.2f}倍")
    print(f"结果一致性: {results_brute == results_opt}")
 
# 执行性能测试
performance_comparison(10000)

在实际测试中，当n=10000时，优化解法的效率通常是暴力搜索法的100倍以上，充分展示了算法优化的重要性。