线性代数理论思维框架

理解《线性代数》的理论思维框架，远比 memorizing 具体的计算方法和公式更重大。一旦掌握了这个框架，你会发现线性代数不再是零散的概念和技巧，而是一个逻辑严密、直观优美的统一整体。

以下是对线性代数理论思维框架的阐述，它将围绕 “空间-映射-分解-表明” 这一核心逻辑链条展开。

线性代数的根本任务是研究线性空间以及保持线性结构（即加法和数乘）的映射（线性变换）。整个理论大厦都建立在这一基础上。

第一阶段：基础概念与直观（具体到抽象）

1. 核心对象：向量 (Vector)

· 直观理解：一开始是箭头（有方向、有长度），后来抽象为更一般的概念（如多项式、矩阵、函数等）。

· 思维关键：跳出“坐标”的束缚。向量是空间中的一个基本元素，坐标只是它在某个特定“坐标系”下的表明。

2. 核心舞台：线性空间 (Vector Space)

· 定义：一个由向量构成的集合，满足加法和数乘的封闭性以及八条公理。

· 思维关键：这是线性代数发生的“宇宙”。我们研究的所有事情都在这个空间里或空间之间发生。例如，二维平面 R²、三维空间 R³，乃至所有 n 次多项式的集合，都是一个线性空间。

3. 核心工具：矩阵 (Matrix)

· 双重身份：

· 数据的排列：一组向量的集合（列向量）。

· 线性变换的表明：这是矩阵更本质的身份。一个矩阵 A 代表了一个从一个空间到另一个空间的线性变换规则 x -> Ax。

第二阶段：两大核心问题（空间的结构与映射的性质）

整个线性代数理论可以看作是围绕两个基本问题构建的：

1. “空间”本身的结构问题：

· 核心概念：线性组合、线性相关/无关、张成空间、基、维数。

· 思维框架：我们如何描述一个线性空间？

· 找到一组线性无关的向量（基），使得空间中的任何向量都可以被它们唯一地线性表明。

· 这组基向量的个数就是空间的维度。

· 意义：基是描述空间的“语言”或“标尺”。一旦选定了基，抽象的向量就有了具体的坐标表明。

2. “空间之间”的映射问题：

· 核心概念：线性变换、像空间、零空间（核）、秩、特征值/特征向量。

· 思维框架：一个线性变换 T 如何改变空间？

· 作用范围：T 能将整个空间“压缩”到多小的一个子空间里？这个子空间的大小就是秩 (Rank)。

· 遗忘效应：T 会把哪些向量“压扁”成零向量？这些向量构成零空间或核 (Null Space/Kernel)。

· 秩-零化度定理：秩 + 零化度 = 原空间维数。这是连接上述两个概念的优美定理，揭示了线性变换的“信息守恒”特性。

第三阶段：理论的升华与统一（分解与对角化）

这是线性代数理论最精彩的部分，它将前面的概念串联起来，目标是简化复杂问题。

1. 特征值 (Eigenvalue) 与特征向量 (Eigenvector)：

· 思维框架：寻找在线性变换 T 下“方向不变”的向量。即 T(v) = λv。

· 意义：特征向量是理解变换的“最佳坐标系”。在特征向量的方向上，变换只是简单的伸缩。

2.对角化 (Diagonalization)：

· 目标：如果能找到一组由特征向量构成的基（特征基），那么线性变换 T 在这组基下的矩阵表明就是一个对角矩阵。

· 思维框架：对角化是将一个复杂的变换分解为一系列沿独立方向（特征方向）的简单伸缩操作。这极大地简化了计算（如计算 A¹⁰⁰）。

3. 更一般的分解思想：

· 不是所有矩阵都能对角化，但可以寻求更一般的分解。

· Schur 分解：任何方阵都可以酉类似于一个上三角矩阵。

· 奇异值分解 (SVD)：这是线性代数的终极统一框架，适用于任何矩阵（甚至非方阵）。

· 思维框架：SVD 告知我们，任何一个线性变换都可以被分解为三个简单操作的连续作用：1) 一个旋转/反射；2) 沿坐标轴方向的伸缩；3) 另一个旋转/反射。

· 意义：SVD 将“空间的结构”和“映射的性质”完美地结合在一起。它同时给出了变换的像空间、零空间、以及它们的正交补空间的一组标准正交基。

第四阶段：几何直观与公理化思维的融合

· 几何直观：始终将向量、线性变换想象成空间中的运动和变形。这能提供强劲的直觉，例如理解行列式是变换对体积的缩放比例，特征值表明拉伸的倍数。

· 公理化思维：当问题抽象到高维或函数空间时，几何直观可能失效，但公理化定义（八条公理）依然坚如磐石。这是线性代数力量强劲的根源——它的结论适用于所有满足公理的线性空间。

我们可以这样概括线性代数的思维旅程：

1. 起点：从求解线性方程组 (Ax = b) 出发。

2. 抽象化：将问题提升到线性空间和线性变换的层面。

3. 分析结构：研究空间的基、维度，以及变换的秩、核。

4. 寻求简化：通过特征分析和矩阵分解（特别是对角化和SVD），将复杂变换拆解为简单操作的组合。

5. 回归应用：利用简化后的模型，优雅地解决实际问题（如方程组求解、数据降维、图像压缩、机器学习等）。

掌握这个框架，你就不仅仅是学会了解题，而是拥有了一个强劲的数学透镜，可以用来观察和理解世界中的许多线性结构。

为了更清晰的理解理论框架，我们来看线性代数理论思维框架绘制的流程图。

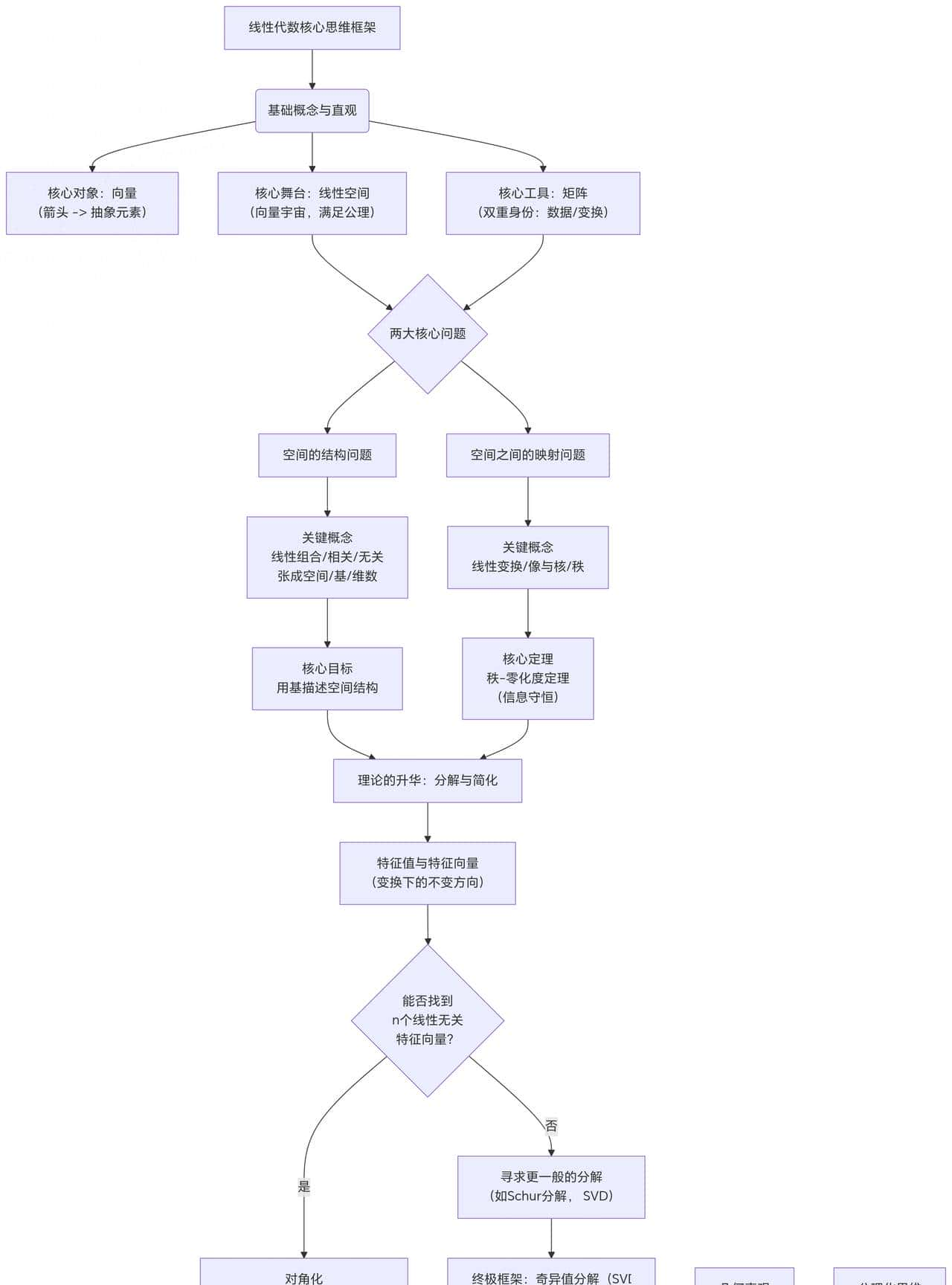
图表解读：

这张图清晰地展示了线性代数理论从基础到核心，再到升华与应用的完整逻辑链条：

1. 从左至右：展示了学习的递进过程，从基础概念到高层应用。

2. 自上而下：展示了理论的层次结构，上层概念是下层概念的基础。

3. 关键节点：

· 两大核心问题：这是整个理论的“承重墙”，将空间本身和空间之间的映射分开研究。

· 理论的升华：分解与简化：这是理论的顶点，旨在将复杂问题转化为简单问题。

· 判断节点（菱形）：展示了根据矩阵性质（能否对角化）走向不同分解路径的逻辑。

· 奇异值分解（SVD）：作为终点前的最终站，它代表了线性代数分析能力的完备性。

· 几何直观与公理化思维：作为两条支撑性的“缆绳”，贯穿始终，为理论提供直觉和严谨性。

这个图表完美地可视化了“空间-映射-分解-表明”的核心框架，希望能协助您更深刻地理解线性代数的内在统一美。