函数零点与方程解：解锁数学难题的钥匙

家人们，在数学的广阔天地里，函数的零点与方程的解就像是一把把神奇的钥匙，能帮我们打开诸多难题的大门。今天，就跟着小景老师的笔记，一起深入探索这个有趣又实用的领域。

图片来源于网络

一元二次方程根的分布：精准定位二次函数零点

咱们先来看看一元二次方程根的分布，也就是二次函数零点的问题。这里面分两种情况。一种是在区间（m,n）上有两个不相等的实根，这需要满足判别式大于零，对称轴在区间内，且区间端点函数值同号等一系列条件。就好比在一场比赛中，选手要满足多个规则才能进入特定环节。举个例子，对于方程x2−3x+2=0x{2}-3x + 2 = 0x2−3x+2=0，在区间（0,3）内就有两个不等实根1和2。

另一种情况是在区间（m,n）上只有一个实根，这时候条件会有所不同。而且，当一元二次方程在区间（m,n）上有根时，求解参数的取值范围也有独特的思路，就像在迷宫中寻找出口，需要按照特定的路线前进。

图片来源于网络

一般函数零点问题解法：多管齐下

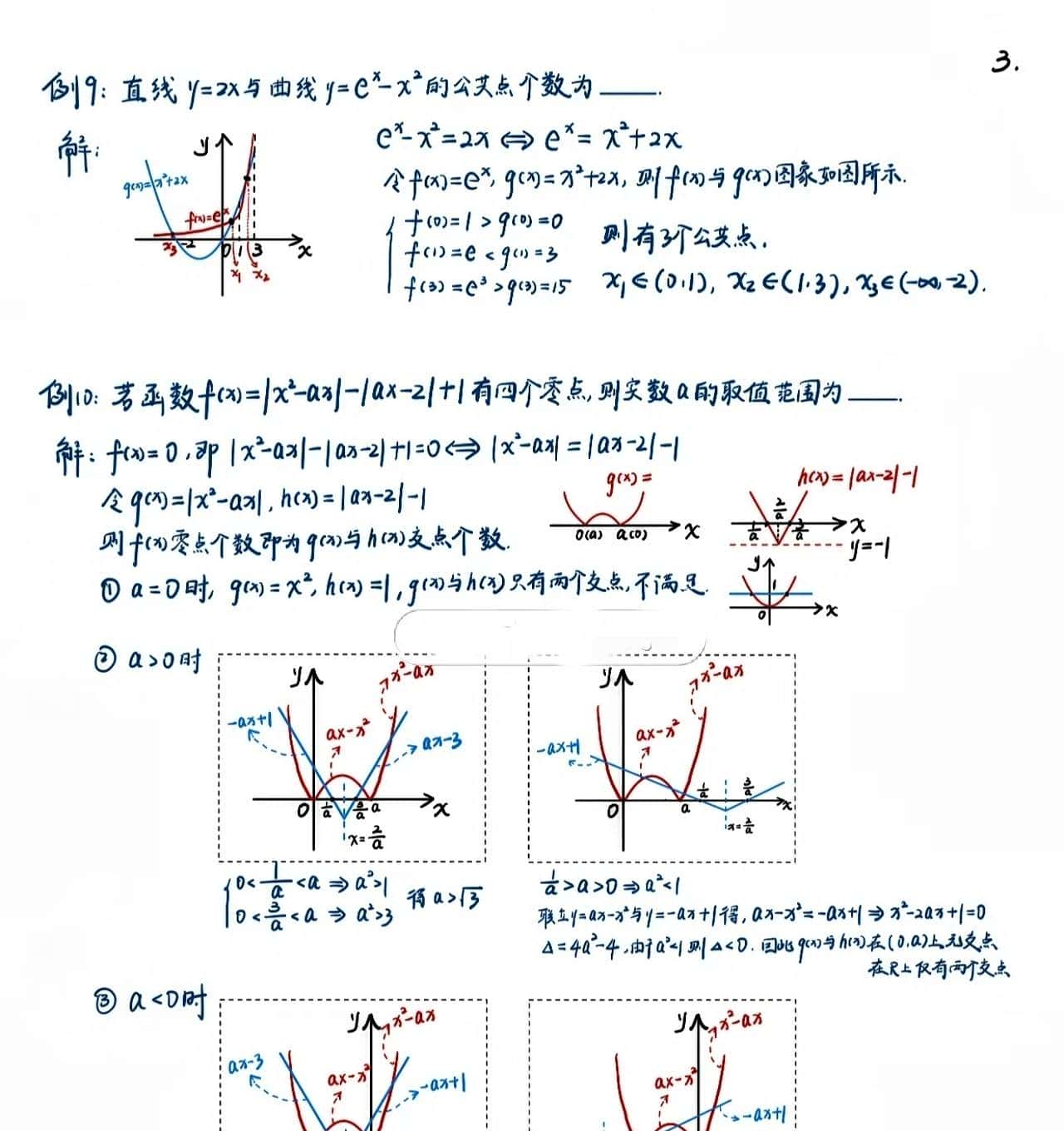
直接解方程：简单粗暴却有效

对于一次、二次函数，我们可以直接根据f(x)=0f(x)=0f(x)=0来求解。这就像解开一道简单的谜题，直接找到答案。列如一次函数y=2x−4y = 2x – 4y=2x−4，令y=0y = 0y=0，就能轻松得出x=2x = 2x=2。

图片来源于网络

零点存在性定理：判断零点的“神兵利器”

函数在区间[a,b][a,b][a,b]连续且f(a)⋅f(b)<0f(a)cdot f(b)<0f(a)⋅f(b)<0时，就存在零点。不过，这可不是绝对的，就像天气预报说可能下雨，但不必定真的会下。我们还需要分析函数的单调性等其他条件，才能更准确地判断零点的情况。

图片来源于网络

画图法：将抽象问题具象化

把函数零点问题转化为曲线交点问题，这是画图法的精髓。我们可以常用参数分离、参数讨论等方法。列如说直线与曲线的零点问题，通过画图能直观地看到它们相交的情况，就像在地图上找到两条路的交汇点。还有含绝对值函数的零点情况分析，画图后也能一目了然。列如函数y=∣x−1∣y=vert x – 1verty=∣x−1∣与y=2y = 2y=2的交点，画图就能轻松找到x=3x = 3x=3和x=−1x = -1x=−1这两个零点。

函数的零点与方程的解在数学的各个领域都有着广泛的应用。掌握了这些方法，就如同拥有了一把万能钥匙，能让我们在数学的海洋中畅游无阻。家人们，赶紧学起来，一起开启数学探索的新征程吧！