一:三类圆周运动模型
►第一类:竖直面内圆周运动(绳、杆模型)
►第二类:水平面内圆周运动的临界问题
►第三类:斜面上圆周运动(倾斜转盘模型)
二:经典题型
题型1 静摩擦力对应的临界问题
题型2 圆锥摆模型及临界问题
题型3 拱桥模型及临界问题
题型4 轻绳模型及临界问题
题型5 轻杆模型及临界问题
题型6 倾斜平面内的临界问题
三:常见临界状态
(1)水平转盘上的物体恰好不发生相对滑动的临界条件是物体与盘间恰好达到最大静摩擦力。
与静摩擦力有关,静摩擦力达到最大值,f≤fmax,fmax=μFN
(2)绳子恰好松弛或被拉断:绳子拉力为零或绳上拉力恰好为最大承受力等。
0≤T≤Tmax
(3)接触面类:与支持面或杆的弹力有关的临界问题:要分析出恰好无支持力这一临界状态下的角速度(或线速度)
FN≥0
四:实例分析
(1)a或b发生相对圆盘滑动的各自临界角速度

Ffmax=μFN=μmg=mω²r,ω=√μg/r。由公式可知,距离圆盘中心远的B物体先发生相对滑动。
(2)两个质量均为m的木块A、B用恰好伸直的轻绳相连,放在水平圆盘上,A恰好处于圆盘中心。

注意:先出现摩擦力后才是拉力.
①轻绳出现拉力的临界角速度:对木块B分析,Ffmax= μmg=mω₁²rB,ω₁=√μg/rB。
②A、B相对圆盘滑动的临界条件:角速度继续增大,绳子出现拉力,B受最大静摩擦力不变,角速度继续增大,A的静摩擦力继续增大,当增大到最大静摩擦力时,A、B相对于转盘开始滑动。
对木块A分析,T=μmg;对木块B分析,T+μmg=mω₂²rB。解得临界角速度为ω₂=√2μg/rB。
结论:当ω≤√μg/rB时,轻绳上拉力为0;当ω≥√2μg/rB时,A、B相对圆盘发生滑动。

(3)两个质量均为m的木块A、B用恰好伸直的轻绳相连,放在水平圆盘上。

①轻绳出现拉力的临界角速度:对木块B分析,Ffmax= μmg=mω₁²rB,ω₁=√μg/rB。
②A、B相对圆盘滑动的临界条件:角速度继续增大,绳子出现拉力,B受最大静摩擦力不变,角速度继续增大,A的静摩擦力继续增大,当增大到最大静摩擦力时,A、B相对于转盘开始滑动。
绳子换成弹簧又怎么分析?

(4)两个质量均为m的木块A、B用恰好伸直的轻绳相连,放在水平圆盘上,A、B恰好处于圆盘中心两侧。

(5)A、B两物块叠放在转盘上
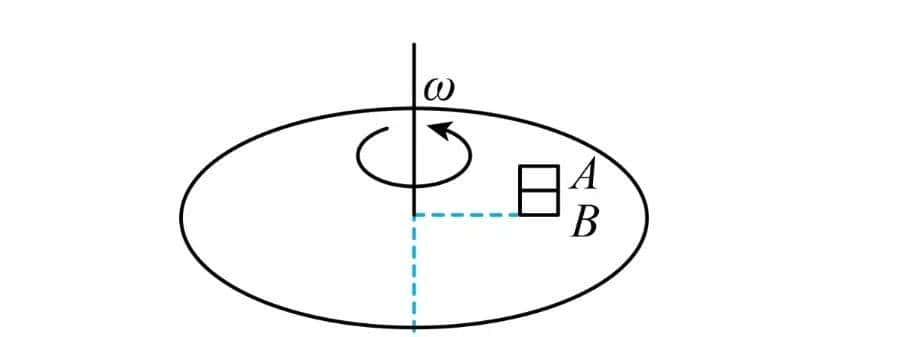
①若μA>μB,则B先相对转盘发生滑动,临界角速度为。
②若μA<μB,则A先相对B发生滑动。
(6)有摩擦力
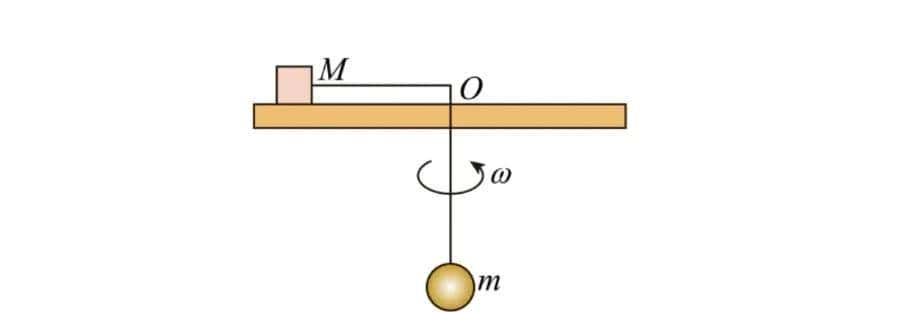
(7)
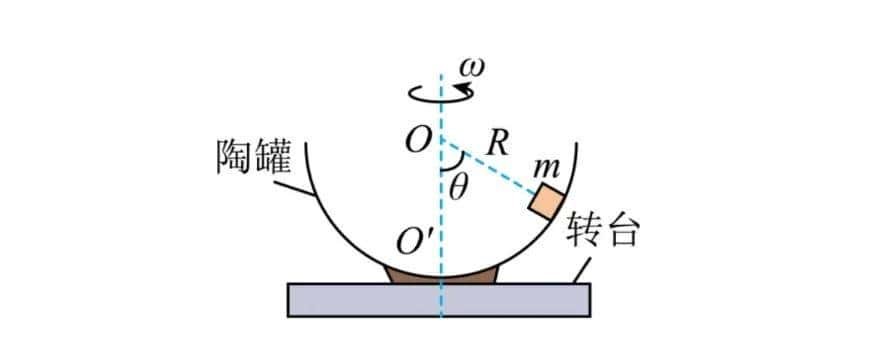
(8)锥面上

(9)锥面类
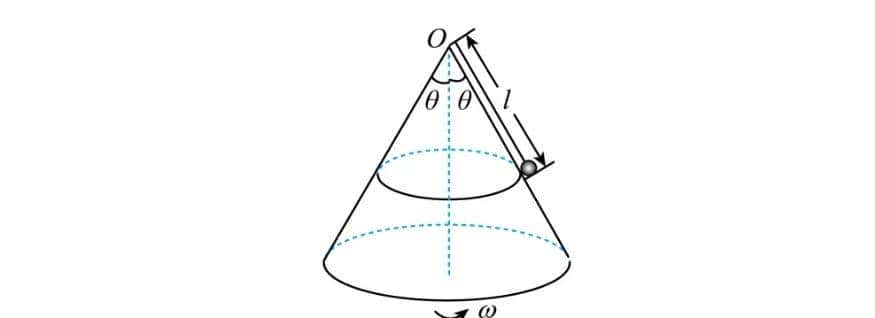
(10)倾斜面上

(11)转筒
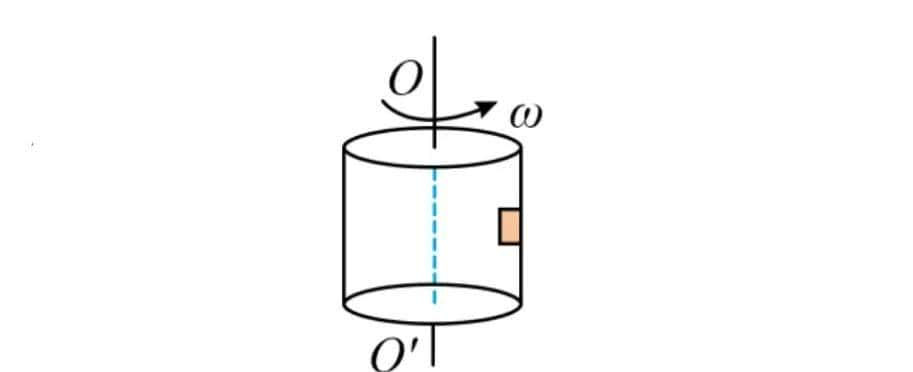
(12)绳子类
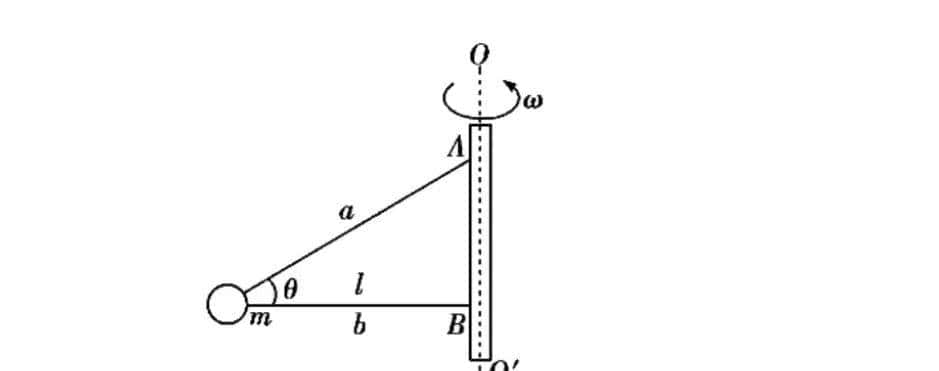














收藏了,感谢分享