通透！决策树 vs 随机森林！！

内容分享6天前发布 Regina饶芮瑜

0 0 0

哈喽，大家好~

今儿和大家分享的是决策树 vs 随机森林。

第一， 决策树 是单一模型，通过一系列轴对齐的划分，把输入空间划分成叶子区域，每个叶子输出类别（或回归值）。

随机森林 是集成模型，对训练集进行有放回抽样，在每棵树的划分处随机子特征子集，训练出大量弱相关的树，再通过投票（分类）或平均（回归）聚合输出。

核心差异上，本质上是偏差-方差与相关性控制：

决策树 ：低偏差（能拟合复杂模式），高方差（对数据扰动敏感），可解释性强，但容易过拟合。

随机森林 ：通过“Bagging + 特征子采样”降低树之间的相关性，显著降低方差，提高泛化；代价是整体可解释性下降、训练/预测成本上升，但性能稳定、鲁棒性强。

核心原理

决策树

划分准则与不纯度 ：

给定训练集，类别集合，在某个节点（样本子集）上，类别的经验频率为

常见不纯度（impurity）度量：

熵（Shannon Entropy）

基尼系数（Gini Impurity）

分类误差（Misclassification Error）

经验上，基尼与熵都常用，二者在决策边界处倾向类似，但熵对低概率类别更敏感。二分类 – 时，，在上与熵趋势相近。

信息增益与CART划分目标 ：

若在节点对特征按阈值进行二分：

加权不纯度为

其中是熵或基尼等不纯度。CART以最小化为目标：

等价地，也可以用不纯度减少（impurity decrease）最大化：

用熵时，信息增益

即等价于互信息。C4.5中还使用增益率（Gain Ratio）以惩罚高基数的划分：

生成树与停止/剪枝 ：

生成树时递归地选择，直到满足停止条件（如最大深度、最小样本数、最小不纯度下降等）。

未剪枝的树一般高度拟合训练集（低偏差高方差）。

CART的代价复杂度剪枝引入结构惩罚：

其中是训练误差或叶节点的不纯度和，是叶子数，控制复杂度惩罚。CART通过“最弱链接剪枝”（weakest link pruning）生成一条子树序列，再用交叉验证选择最佳对应的子树。

预测与概率估计 ：

分类：叶节点取多数类

概率估计（频率）：

回归：取叶子样本均值

特征重大性（MDI） ：

基于不纯度减少的特征重大性（Mean Decrease Impurity, MDI）：

对每个用到特征的节点累加加权不纯度下降。注意MDI可能对高基数/连续特征存在偏好，Permutation Importance可作为补充。

随机森林

Bagging 与 OOB ：

Bagging通过Bootstrap采样构造个训练子集：

对原始数据，每棵树随机有放回抽样次得到；
对每棵树训练一个尽量强但高方差的基学习器（一般为未剪枝或弱剪枝树）；
聚合预测：分类采用多数投票，回归采用平均。

每个样本在一次bootstrap后“未被抽中”的概率为

因此约36.8%的样本对某棵树是袋外样本（OOB）。OOB可用作无偏验证：对样本，仅用未包含的树对其预测，得到OOB预测，估计OOB误差作为泛化误差近似。

随机子特征 ：

在每个分裂节点，仅在随机选择的个特征上搜索最优划分，典型取值：

分类：
回归：这一步进一步去相关化树之间的决策，使集成方差下降更明显。

方差-相关性分解 ：

设单棵树预测为，其方差为，任意两棵树预测的相关系数为。随机森林平均预测

则其方差为（Breiman经典近似）

可见当时，方差下界为，因此降低树间相关性比单纯增加更关键；随机子特征正是为此设计。

Margin、Strength 与泛化界 ：

对分类问题，定义随机森林在样本上的margin为

其中是由随机机制（bootstrap与特征子采样）生成的一棵树，表明对随机性的概率。随机森林的“强度”（strength）定义为

Breiman给出基于平均相关性与强度的泛化误差上界（直观表达）：

该式强调：提高单树强度（更强的基学习器）与降低树间相关性共同决定RF的泛化能力。

OOB 误差与概率估计 ：

OOB 预测通过仅使用不包含样本的子模型集合：

OOB误差近似CV误差，且几乎无计算开销（训练过程中自然得到），是调参的重大指标。

RF 的特征重大性与Permutation ：

MDI：对森林中所有树的MDI求平均。

Permutation Importance：随机置乱特征在验证集或OOB集上的取值，度量性能下降

Permutation重大性能缓解MDI的某些偏差，也能发现强交互但单独贡献不显著的特征。

决策树 vs 随机森林

我们从下面6个方面，详细的阐述其中的核心区别：

解释性

决策树：路径清晰，可转化为规则，单模型可视化直观；适合需要“可审计”的场景。
随机森林：整体可解释性弱（许多树），但可用特征重大性、局部解释方法（如SHAP）辅助。

性能与稳定性

决策树：易过拟合，对数据扰动敏感，性能波动较大。
随机森林：鲁棒稳定，一般显著优于单树，尤其在有噪声和高维情况下。

计算与资源

决策树：训练/预测快，参数少，适合轻量场景或在线快速决策。
随机森林：训练耗时与内存开销更大（多棵树），但可并行；预测时延较高。

小样本/大样本

小样本：决策树与随机森林都可能受限，但RF的Bagging与OOB可更好地稳定估计。
大样本：RF一般表现更好，且可扩展并行。

特征工程与缺失 ：两者对非线性、类别特征（经适度编码）与异常值较鲁棒；RF更能平衡噪声与泛化。

类别不平衡 ：均可使用类权重/重采样；RF的OOB分层评估更便于调参。

完整案例

这里我们用一个二维非线性可分的数据集进行分类，对比决策树与随机森林的行为差异。

代码的几个核心点：

决策边界展示模型对输入空间划分的形态，观察过拟合/平滑程度；
ROC对比展示整体判别能力；
OOB误差曲线展示RF的“内置交叉验证”特性和随树数增长的稳定收敛；
特征重大性展示RF在当前数据上对特征的依赖度。

importnumpyasnp
importmatplotlib.pyplotasplt
importseabornassns
fromsklearn.datasetsimportmake_moons
fromsklearn.model_selectionimporttrain_test_split
fromsklearn.treeimportDecisionTreeClassifier
fromsklearn.ensembleimportRandomForestClassifier
fromsklearn.metricsimportroc_curve, auc, accuracy_score, confusion_matrix
frommatplotlib.colorsimportListedColormap
frommpl_toolkits.axes_grid1.inset_locatorimportinset_axes

# 1. 数据集
np.random.seed(42)
X, y = make_moons(n_samples=1200, noise=0.30, random_state=42)

X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.30, random_state=42, stratify=y
)

# 2. 训练决策树
dt = DecisionTreeClassifier(
criterion="gini",
max_depth=None,# 放开深度让树尽量拟合
min_samples_leaf=1,
random_state=42
)
dt.fit(X_train, y_train)

# 3. 训练随机森林（使用OOB估计）
rf = RandomForestClassifier(
n_estimators=200,
max_features="sqrt",
bootstrap=True,
oob_score=True,
random_state=42,
n_jobs=-1
)
rf.fit(X_train, y_train)

# 4. 性能评估
y_score_dt = dt.predict_proba(X_test)[:,1]
y_score_rf = rf.predict_proba(X_test)[:,1]

fpr_dt, tpr_dt, _ = roc_curve(y_test, y_score_dt)
fpr_rf, tpr_rf, _ = roc_curve(y_test, y_score_rf)
auc_dt = auc(fpr_dt, tpr_dt)
auc_rf = auc(fpr_rf, tpr_rf)

y_pred_dt = dt.predict(X_test)
y_pred_rf = rf.predict(X_test)
acc_dt = accuracy_score(y_test, y_pred_dt)
acc_rf = accuracy_score(y_test, y_pred_rf)

# 5. 为决策边界生成网格
defmake_meshgrid(X, h=0.02, padding=0.6):
x_min, x_max = X[:,0].min - padding, X[:,0].max + padding
y_min, y_max = X[:,1].min - padding, X[:,1].max + padding
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
returnxx, yy

xx, yy = make_meshgrid(X, h=0.02)

Z_dt = dt.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
Z_rf = rf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

# 6. 计算OOB误差随n_estimators变化（避免太小导致警告）
n_list = [10,20,40,70,100,150,200,300,400]
oob_errors = 
forninn_list:
rf_tmp = RandomForestClassifier(
n_estimators=n, max_features="sqrt", bootstrap=True,
oob_score=True, random_state=42, n_jobs=-1
)
rf_tmp.fit(X_train, y_train)
oob_error =1.0- rf_tmp.oob_score_
oob_errors.append(oob_error)

# 7. 可视化分析
fig, axes = plt.subplots(2,2, figsize=(16,12))
plt.subplots_adjust(wspace=0.18, hspace=0.22)

custom_cmap = ListedColormap(["#FF1493", "#00CED1"])

# 子图1：决策树决策边界
ax = axes[0,0]
cmap_bg_dt = sns.color_palette("cool", as_cmap=True)
ax.contourf(xx, yy, Z_dt, alpha=0.75, cmap=cmap_bg_dt)
ax.scatter(X_test[:,0], X_test[:,1], c=y_test, s=30, cmap=custom_cmap, edgecolors="k")
ax.set_title(f"决策树 决策边界
Test Acc={acc_dt:.3f}, AUC={auc_dt:.3f}", color="#2E8B57", fontsize=14)
ax.set_xlabel("x1"); ax.set_ylabel("x2")

# 子图2：随机森林决策边界
ax = axes[0,1]
cmap_bg_rf = sns.color_palette("plasma", as_cmap=True)
ax.contourf(xx, yy, Z_rf, alpha=0.75, cmap=cmap_bg_rf)
ax.scatter(X_test[:,0], X_test[:,1], c=y_test, s=30, cmap=custom_cmap, edgecolors="k")
ax.set_title(f"随机森林 决策边界（OOB={rf.oob_score_:.3f}）
Test Acc={acc_rf:.3f}, AUC={auc_rf:.3f}", color="#8A2BE2", fontsize=14)
ax.set_xlabel("x1"); ax.set_ylabel("x2")

# 子图3：ROC曲线对比
ax = axes[1,0]
ax.plot(fpr_dt, tpr_dt, color="#FF1493", lw=3, label=f"决策树 ROC (AUC={auc_dt:.3f})")
ax.plot(fpr_rf, tpr_rf, color="#00CED1", lw=3, label=f"随机森林 ROC (AUC={auc_rf:.3f})")
ax.plot([0,1], [0,1], "k--", lw=1, label="随机猜测")
ax.set_xlim([0.0,1.0]); ax.set_ylim([0.0,1.05])
ax.set_xlabel("假阳性率 FPR"); ax.set_ylabel("真阳性率 TPR")
ax.set_title("ROC 对比：RF 一般更稳健", color="#B22222", fontsize=14)
ax.legend(loc="lower right")

# 子图4：OOB误差 vs 树数量 + Inset 特征重大性
ax = axes[1,1]
ax.plot(n_list, oob_errors, marker="o", color="#FF8C00", lw=3)
ax.set_xlabel("树的数量 (n_estimators)")
ax.set_ylabel("OOB误差")
ax.set_title("随机森林 OOB误差随树数变化（越小越好）", color="#006400", fontsize=14)
ax.grid(True, alpha=0.3)

# Inset: 特征重大性
inset_ax = inset_axes(ax, width="45%", height="55%", loc="upper right", borderpad=1.2)
feat_names = ["x1", "x2"]
importances_rf = rf.feature_importances_
colors_bar = ["#FF1493", "#00CED1"]
inset_ax.bar(feat_names, importances_rf, color=colors_bar, edgecolor="k")
inset_ax.set_title("RF 特征重大性", fontsize=10)
inset_ax.set_ylim(0, max(0.01, importances_rf.max*1.2))
inset_ax.tick_params(axis='x', labelrotation=0, labelsize=9)

plt.suptitle("决策树 vs 随机森林：边界、ROC、OOB与特征重大性（虚拟数据）", fontsize=18, y=0.98)
plt.show

# 输出混淆矩阵与结果
cm_dt = confusion_matrix(y_test, y_pred_dt)
cm_rf = confusion_matrix(y_test, y_pred_rf)
print("决策树：Test Acc=", acc_dt, "AUC=", auc_dt)
print("混淆矩阵：
", cm_dt)
print("随机森林：Test Acc=", acc_rf, "AUC=", auc_rf, "OOB=", rf.oob_score_)
print("混淆矩阵：
", cm_rf)

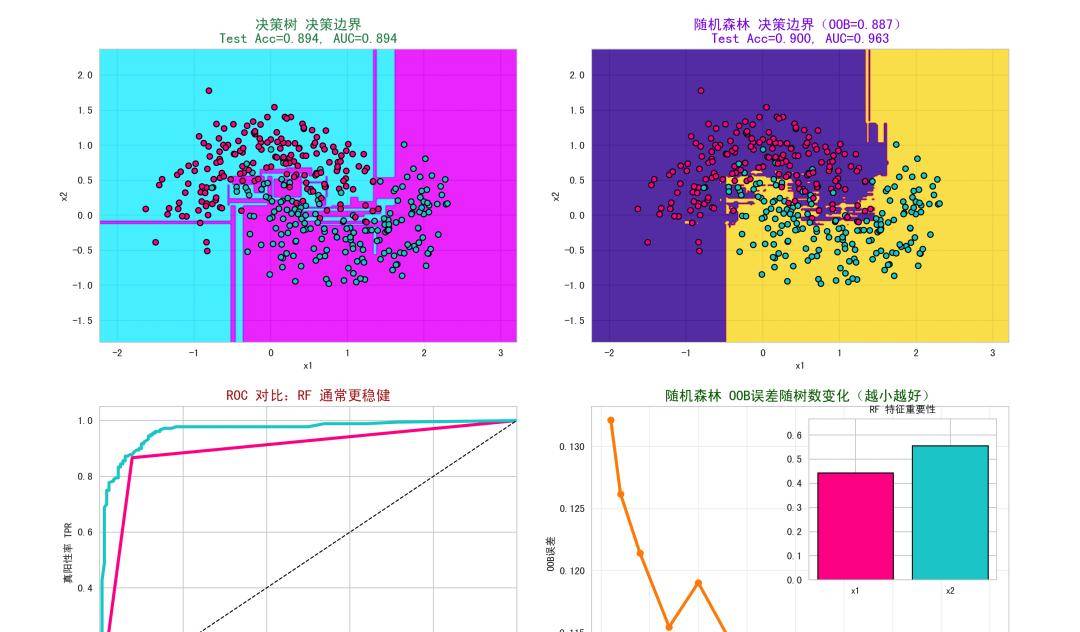
图1：决策树的决策边界 ：可见边界呈现“块状/阶梯状”的轴对齐划分，容易在噪声处产生锯齿形复杂边界，反映了单树高方差、易过拟合的特性。当样本噪声较大时，单树容易把局部噪声当作模式记住，导致测试集性能波动。

图2：随机森林的决策边界 ：边界较为平滑、稳定，避免过多微小摆动；这是通过Bagging和特征子采样实现的方差降低和去相关化效果。标题中展示OOB分数，往往与测试集指标接近，是可替代的无偏泛化评估。

图3：ROC曲线对比 ：随机森林的AUC一般高于单树，曲线更靠近左上角，表明其整体判别能力更强、阈值选择鲁棒性更好。在非线性可分数据上，RF对局部异常值不敏感，具有更好的全局性能。

图4：OOB误差 vs 树数 + Inset特征重大性 ：OOB误差随树的数量增加快速下降并趋于稳定，体现出RF随着集成规模增长而逐步收敛、方差减小的特性。Inset中的特征重大性（MDI）展示了RF在当前数据上对两个特征的依赖程度。对于make_moons，两维特征都重大，权重可能近似均衡。

通透！决策树 vs 随机森林！！