基于对称最优法的BLDC转速环PI控制器设计深度解析

1. 引言

直流无刷电机（BLDC）因其高功率密度、高效率等优点，在工业控制领域获得了广泛应用。其控制性能很大程度上取决于转速环的控制效果。本文将基于BLDC的dq模型，深入探讨采用对称最优法设计转速环PI参数的原理与实现方法。

我们将从BLDC的数学模型出发，分析转速环的控制结构，重点阐述对称最优法的理论基础、设计步骤和参数整定方法，并针对采样频率25kHz、电流环简化为一阶惯性环节的实际条件，提供详细的设计实例。

---

2. BLDC的dq模型与转速环结构

2.1 dq坐标系下的BLDC数学模型

在dq同步旋转坐标系下，BLDC的电压方程可表示为：

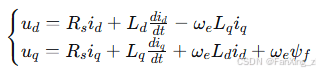
其中，、为d、q轴电压，、为d、q轴电流，、为d、q轴电感，为定子电阻，为永磁体磁链，为电角速度。

电磁转矩方程为：

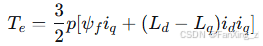
对于面装式永磁同步电机（SPMSM），，转矩方程简化为：

其中，为转矩常数，为极对数。

2.2 转速环控制结构

转速环通常作为外环，其输出作为q轴电流的给定值，控制框图如下：

转速给定ω* → 转速控制器 → iq* → 电流环 → 电机 → 实际转速ω
                ↑                        |
                +------------------------+

转速控制器的设计目标是使实际转速快速、准确地跟踪给定值，同时保证系统的稳定性和鲁棒性。

---

3. 对称最优法理论基础

3.1 对称最优法的基本思想

对称最优法（Symmetrical Optimum Method）是一种基于频域设计的控制器参数整定方法，特别适用于具有惯性环节的系统。其核心思想是通过合理选择控制器参数，使系统的开环频率特性在截止频率附近呈现对称特性，从而获得较好的动态性能和稳定裕度。

3.2 典型系统结构

考虑电流环简化为一阶惯性环节的情况，电流环的传递函数为：

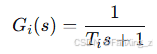
其中，为电流环等效时间常数。

电机机械运动方程为：

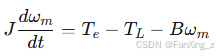
其中，为转动惯量，为负载转矩，为粘滞摩擦系数。

忽略负载转矩和摩擦，从q轴电流到机械转速的传递函数为：

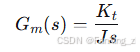
因此，转速环的被控对象传递函数为：

---

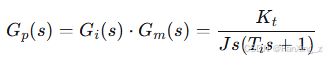
4. 转速环PI控制器设计

4.1 PI控制器形式

转速环采用PI控制器，其传递函数为：

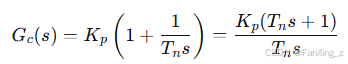
其中，为比例系数，为积分时间常数。

4.2 开环传递函数

系统开环传递函数为：

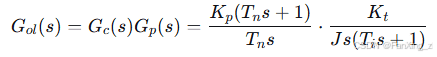
整理得：

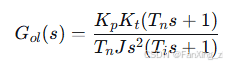
4.3 对称最优法设计准则

对称最优法的设计准则如下：

相位裕度最大化：通过合理选择参数，使系统在截止频率处具有最大相位裕度

幅频特性对称：在附近，幅频特性曲线近似对称

参数关系：选择积分时间常数，其中为设计参数

4.4 参数整定过程

根据对称最优法，按以下步骤整定PI参数：

步骤1：确定积分时间常数

选择，通常取，本文取：

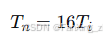
步骤2：计算比例系数

根据对称最优法，开环传递函数在截止频率处的幅值应为1：

将代入开环传递函数：

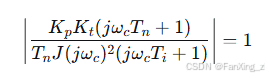
在截止频率处，有，（合理选择），近似可得：

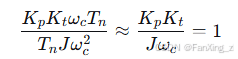
因此：

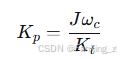
根据对称最优法理论，最佳截止频率为：

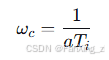
代入得：

最终得到比例系数：

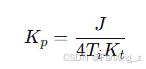
步骤3：计算积分系数

积分系数与积分时间常数的关系为：

---

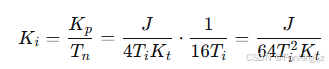
5. 考虑数字实现的离散化

5.1 离散PI控制器

在数字控制系统中，需要将连续PI控制器离散化。采用双线性变换（Tustin变换），令，其中为采样周期。

PI控制器的离散形式为：

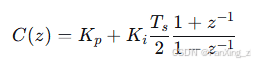
5.2 离散化实现

给定采样频率25kHz，采样周期$T_s = 40mu s$。

位置式PI算法：

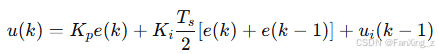
其中，为上一次的积分项输出。

增量式PI算法：

---

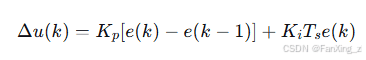
6. 设计实例与性能分析

6.1 系统参数假设

假设系统参数如下：

转动惯量

转矩常数

电流环时间常数

设计参数

6.2 PI参数计算

根据前述公式：

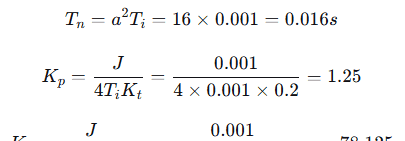
6.3 性能指标分析

相位裕度：

开环传递函数在截止频率处的相位为：

代入，，：

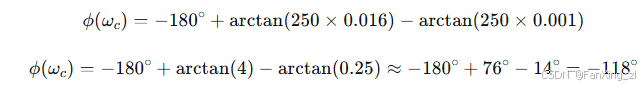
相位裕度，满足一般工业应用要求（）。

超调量：

对称最优法设计的系统通常会有一定的超调量，约为30%40%。如需减小超调，可采取以下措施：

增加设计参数的值

加入设定值滤波器

采用变参数PI控制

---

7. 实际应用考虑

7.1 抗饱和处理

在实际系统中，需要考虑输出限幅和抗饱和处理。常用的抗饱和方法有：

积分分离：当误差较大时，取消积分作用

抗饱和补偿：当输出饱和时，停止积分或减小积分量

条件积分：仅在特定条件下进行积分

7.2 参数鲁棒性

对称最优法设计的控制器对系统参数变化具有一定的鲁棒性，但当$J$、$K_t$等参数变化较大时，仍需考虑：

在线参数辨识

自适应控制

鲁棒控制方法

7.3 数字实现注意事项

量化误差：注意ADC分辨率和计算字长

计算延时：考虑算法执行时间和PWM更新时机

抗混叠滤波：转速测量需加入合适的滤波

---

8. 总结

本文详细介绍了基于对称最优法的BLDC转速环PI控制器设计方法，主要贡献包括：

建立了BLDC的dq模型和转速环控制结构

深入阐述了对称最优法的理论基础和设计准则

推导了PI参数的解析表达式

提供了考虑数字实现的离散化方法

通过设计实例验证了方法的有效性

对称最优法作为一种系统化的控制器设计方法，在BLDC控制中具有重要应用价值。通过合理选择设计参数，可以在保证系统稳定性的同时，获得满意的动态性能。

---

参考文献

Krishnan, R. (2001). Electric Motor Drives: Modeling, Analysis, and Control. Prentice Hall.

Bose, B. K. (2002). Modern Power Electronics and AC Drives. Prentice Hall.

阮毅, 陈伯时. (2010). 电力拖动自动控制系统. 机械工业出版社.

*版权声明：本文为原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。*