1、时序差分(TD)与贝尔曼方程的关系
时序差分(Temporal Difference, TD)方法与贝尔曼方程是强化学习中理论与算法的核心结合。贝尔曼方程提供了值函数的递归数学定义,而 TD 方法则是通过采样数据来逼近这一方程的解。两者的关系可以从以下四个层面理解:
(1) 贝尔曼方程:理论基石
贝尔曼方程是强化学习中最基础的数学工具,它定义了状态值函数 V(s)或动作值函数 Q(s,a) 的递归关系:

- 核心思想:当前状态的值等于即时奖励加上后续状态的折扣值的期望。
- 作用:为值函数提供了严格的数学定义,是动态规划(DP)和时序差分(TD)的共同理论基础。
(2)TD 方法:贝尔曼方程的采样实现
TD 方法通过实际交互的样本数据,用单步或几步经验近似贝尔曼方程中的期望值,从而避免了对环境模型(状态转移概率 p(s′∣s,a)的依赖。
- TD 更新公式(以 TD(0) 为例):

(3)TD 是贝尔曼方程的随机近似算法
贝尔曼方程的解是值函数的理想值,而 TD 方法通过以下步骤逼近这一解:
- 采样替代期望:用实际交互的单步样本 (St,At,Rt+1,St+1)取代贝尔曼方程中的期望计算。
- 迭代更新:逐步调整值函数估计,使 TD 误差最小化。
- 收敛性:在 Robbins-Monro 条件下(如适当衰减的学习率 α),TD 方法能收敛到贝尔曼方程的解。
(4)总结
- 贝尔曼方程:定义了值函数的递归数学关系,是强化学习的理论核心。
- TD 方法:通过采样和迭代更新,将贝尔曼方程中的期望计算转化为实际可行的无模型学习算法。
- 核心关系:
- TD 方法是贝尔曼方程的随机近似实现。
- TD 的更新目标直接对应贝尔曼方程的右侧期望项。
- TD 的收敛性依赖于贝尔曼方程的理论保证。
通过这种关系,TD 方法在无模型、高维状态空间中实现了高效学习,成为强化学习中最广泛应用的算法家族之一。
2、时序差分(TD)、贝尔曼方程与马尔可夫性质的关系
在强化学习中,马尔可夫性质是时序差分(TD)方法、贝尔曼方程以及大多数经典强化学习算法的核心基础。三者的关系可以总结为:
马尔可夫性质是理论前提 → 贝尔曼方程是数学工具 → TD方法是实践算法。
(1)马尔可夫性质:一切的基础
- 定义
马尔可夫性质(Markov Property)表明:未来状态仅依赖于当前状态和动作,与历史无关。数学表述为:
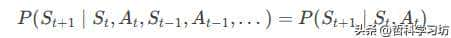
- 作用
简化问题:将复杂的历史依赖简化为仅当前状态的依赖。
支撑MDP框架:马尔可夫决策过程(MDP)假设环境满足马尔可夫性质,是强化学习的标准建模工具。
(2)贝尔曼方程:马尔可夫性的数学体现
贝尔曼方程的成立直接依赖马尔可夫性质。以状态值函数为例:
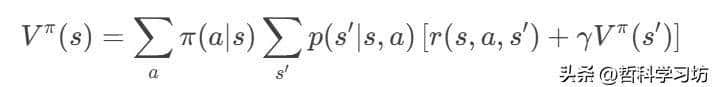
马尔可夫性的体现
- 状态转移独立性:下一状态 s′仅依赖当前状态 s和动作 a,而非历史。
- 递归分解:长期回报 Vπ(s)被分解为即时奖励 r和后续状态的折扣值 γVπ(s′)。
- 动态规划可行性:若无马尔可夫性,无法将全局问题递归分解为局部子问题。
(3)TD方法:马尔可夫性下的无模型学习
TD方法(如Q-Learning、SARSA)是贝尔曼方程的无模型实现,其有效性同样依赖马尔可夫性。
TD更新的马尔可夫性依赖
- 单步更新:TD利用当前状态 st、动作 at、奖励 rt+1 和下一状态 st+1 进行更新。
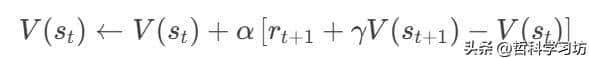
- 下一状态 st+1 仅由 st 和 at 决定(马尔可夫性)。
- 若环境不满足马尔可夫性(如部分可观测问题),TD的更新目标将包含隐藏的历史信息误差。
(4)总结
- 马尔可夫性质是强化学习的基石,确保状态转移和值函数递归分解的合理性。
- 贝尔曼方程是马尔可夫性下的数学工具,定义值函数的动态关系。
- TD方法是贝尔曼方程的无模型实现,依赖马尔可夫性通过采样高效学习。
三者关系链:
马尔可夫性 → 贝尔曼方程 → TD方法
若环境不满足马尔可夫性,这一链条将断裂,需调整状态表明或算法设计(如使用RNN、POMDP)。
3、满足与不满足马尔可夫性质的环境对比
(1)满足马尔可夫性质的环境
定义:未来状态仅依赖当前状态和动作,与历史无关。
特点:
- 状态完整性:当前状态包含所有影响未来状态的信息。
- 明确状态转移概率:下一状态仅由当前状态和动作决定,可用 p(s′∣s,a)p(s′∣s,a) 描述。
示例:
- 棋盘游戏(如国际象棋):
- 当前棋盘布局(状态)完全决定下一步所有可能走法。
- 无需思考之前的落子顺序,只需当前布局即可决策。
- 机器人导航(确定性环境):
- 机器人当前位置和动作(如“向左”)明确决定下一位置。
- 例如:网格世界中,移动指令直接对应坐标变化。
- 简单赌博机(Bandit):
- 每次拉臂的奖励仅由当前选择的臂决定,与之前的选择无关。
(2)不满足马尔可夫性质的环境
定义:未来状态依赖历史信息,而非仅当前状态和动作。
特点:
- 状态信息缺失:当前状态未捕获所有影响未来的关键因素。
- 历史依赖性强:需通过历史状态或动作预测未来。
示例:
- 部分可观测环境(POMDP):
- 真实状态:满足马尔可夫性,但智能体无法完全观测。
- 观测状态:因信息缺失导致非马尔可夫性。
- 例子:
- 机器人通过噪声传感器获取环境信息(如模糊的摄像头画面)。
- 扑克游戏中,玩家无法看到对手的手牌(隐藏信息)。
- 时间序列依赖任务:
- 股票价格预测:未来价格依赖长期趋势(如过去30天的均线)。
- 自然语言处理:句子的语义依赖上文所有词语(需LSTM/Transformer建模长程依赖)。
- 资源消耗型任务:
- 电池供电机器人:移动成功率受剩余电量影响,但电量未纳入状态。
- 库存管理:未来需求依赖季节性历史销售数据,但状态仅包含当前库存。
(3)判断标准
|
标准 |
满足马尔可夫性 |
不满足马尔可夫性 |
|
状态完整性 |
当前状态包含所有关键信息 |
状态缺失关键历史或隐藏信息 |
|
转移概率依赖 |
仅依赖 (s,a)(s,a) |
依赖历史轨迹 (s0,a0,…,st)(s0,a0,…,st) |
|
值函数更新 |
可用贝尔曼方程递归分解 |
需扩展状态或使用记忆机制 |
|
典型算法适用性 |
TD、Q-Learning、DP |
RNN、POMDP、DRQN |
(4)总结
- 满足马尔可夫性:环境动态完全由当前状态和动作决定,适合经典强化学习算法(如TD、Q-Learning)。
- 不满足马尔可夫性:需扩展状态表明或引入记忆机制,常见于部分可观测、时间序列依赖或资源消耗型任务。
- 核心区别:状态的完整性和历史依赖性决定了马尔可夫性质是否成立。
以下是一个结合 马尔可夫性质、贝尔曼方程 和 时序差分(TD) 的 Python 程序示例,通过一个简单的网格世界环境,展示它们的核心关系:
程序目标
- 马尔可夫性质:环境状态转移仅依赖当前状态和动作。
- 贝尔曼方程:通过动态规划(DP)迭代计算状态值函数。
- TD方法:通过采样轨迹在线更新值函数。
- 对比DP与TD:验证两者在马尔可夫环境下的收敛一致性。
import numpy as np
import matplotlib.pyplot as plt
# ====================== 环境定义(马尔可夫性质) ======================
class GridWorld:
"""4x4网格世界,终点在右下角,移动奖励-0.1,到达终点奖励+1"""
def __init__(self):
self.size = 4
self.terminal = (3, 3)
self.actions = ['up', 'down', 'left', 'right']
def step(self, state, action):
"""马尔可夫性质:下一状态仅依赖当前状态和动作"""
i, j = state
if action == 'up':
next_i = max(i - 1, 0)
next_j = j
elif action == 'down':
next_i = min(i + 1, self.size - 1)
next_j = j
elif action == 'left':
next_i = i
next_j = max(j - 1, 0)
elif action == 'right':
next_i = i
next_j = min(j + 1, self.size - 1)
next_state = (next_i, next_j)
# 奖励函数
reward = 1.0 if next_state == self.terminal else -0.1
return next_state, reward
# ====================== 动态规划(贝尔曼方程求解) ======================
def bellman_dp(env, gamma=0.9, theta=1e-4):
"""贝尔曼方程迭代求解状态值函数"""
V = np.zeros((env.size, env.size))
policy = np.ones((env.size, env.size, len(env.actions))) / len(env.actions) # 均匀随机策略
while True:
delta = 0
for i in range(env.size):
for j in range(env.size):
if (i, j) == env.terminal:
continue
v_old = V[i, j]
v_new = 0
for a_idx, action in enumerate(env.actions):
next_state, reward = env.step((i, j), action)
next_i, next_j = next_state
# 贝尔曼方程求和:Σπ(a|s)Σp(s'|s,a)[r + γV(s')]
v_new += policy[i, j, a_idx] * (reward + gamma * V[next_i, next_j])
V[i, j] = v_new
delta = max(delta, abs(v_old - V[i, j]))
if delta < theta:
break
return V
# ====================== 时序差分(TD(0)学习) ======================
def td_learning(env, gamma=0.9, alpha=0.1, episodes=100):
"""TD(0)在线更新值函数"""
V = np.zeros((env.size, env.size))
for _ in range(episodes):
state = (0, 0) # 起点
while state != env.terminal:
# 随机选择动作(均匀策略)
action = np.random.choice(env.actions)
next_state, reward = env.step(state, action)
i, j = state
next_i, next_j = next_state
# TD更新:V(s) ← V(s) + α[r + γV(s') - V(s)]
V[i, j] += alpha * (reward + gamma * V[next_i, next_j] - V[i, j])
state = next_state
return V
# ====================== 运行与可视化 ======================
if __name__ == "__main__":
env = GridWorld()
# 动态规划求解
V_dp = bellman_dp(env)
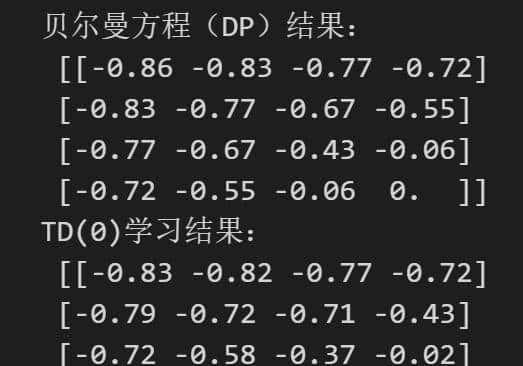
print("贝尔曼方程(DP)结果:
", np.round(V_dp, 2))
# TD学习
V_td = td_learning(env, episodes=1000)
print("TD(0)学习结果:
", np.round(V_td, 2))
# 可视化对比
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.imshow(V_dp, cmap='hot')
plt.title("Dynamic Programming (Bellman)")
plt.colorbar()
plt.subplot(1, 2, 2)
plt.imshow(V_td, cmap='hot')
plt.title("TD(0) Learning")
plt.colorbar()
plt.show()代码解析
1. 马尔可夫性质
- 环境类 GridWorld:
- step 方法实现状态转移,下一状态仅依赖当前状态和动作(无历史依赖)。
- 例如:在状态 (1,1) 执行动作 “right” 后,必然转移到 (1,2)。
2. 贝尔曼方程(动态规划)
- 函数 bellman_dp:
- 遍历所有状态,通过贝尔曼方程迭代更新值函数:
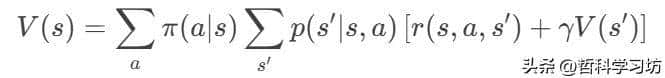
- 收敛条件:值函数变化小于阈值 theta。
3. 时序差分(TD(0))
- 函数 td_learning:
- 通过采样轨迹在线更新值函数:
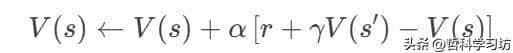
- 体现马尔可夫性:仅用当前状态和动作生成下一状态。
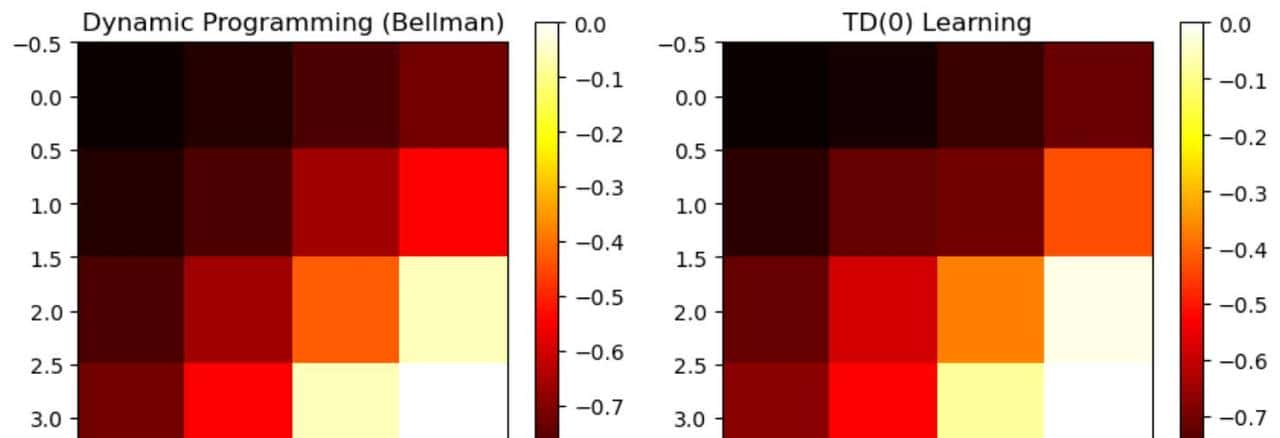
4. 可视化对比
- 热力图显示 DP 和 TD 学习到的值函数:
- DP 直接求解贝尔曼方程(准确解)。
- TD 通过采样逼近贝尔曼方程(近似解)。
相关文章