电磁感应综合题是高二物理期中后及期末的核心拉分题型，学生在解题时常因 “安培力方向判断错误（正确率仅 52%）、能量方程漏项、电路电阻忽略内阻” 这三类问题导致失分。本文聚焦力电结合与能量转化两大高频考查方向，通过梳理核心题型特征、建立 “四步解题法”“三大能量关系” 等标准化流程，搭配左手定则实操技巧与避坑指南，助力学生经 5 天专项训练，从基础平衡题型逐步过渡到动态综合题型，最终实现综合题正确率提升至 80% 以上，为期末电磁学压轴题突破奠定基础。

一、电磁感应综合题：核心题型分类与共性公式链

电磁感应综合题的本质是 “电磁现象与力学规律、能量规律的结合”，高频题型可划分为三类，且所有题型均围绕 “感应电动势→感应电流→安培力” 的核心公式链展开，这一公式链是连接电磁学与力学、能量学的关键桥梁。

1. 三大高频题型特征与解题关键

力电平衡类：此类题型的核心特征是导体棒做匀速运动或匀变速运动，安培力需与拉力、重力分力、摩擦力等其他力达到平衡状态（合力为零或恒定）。常见的真题示例场景包括水平导轨上导体棒受恒力匀速运动，以及斜面导轨上导体棒匀速下滑或上滑。解题的关键规律是牛顿第二定律 —— 当导体棒匀速运动时，合力F_{å}=0；当导体棒做匀变速运动时，合力F_{å}=ma。

能量守恒类：该类题型中，导体棒运动过程伴随机械能与电能的相互转化，安培力做功的绝对值等于电路中产生的焦耳热（即能量损耗）。真题示例场景有导体棒沿光滑斜面下滑切割磁感线（重力势能转化为动能与焦耳热）、水平导轨上导体棒受拉力运动（拉力做功转化为动能与焦耳热）。解题核心是能量守恒定律，即机械能的变化量等于电能的变化量，且电能的变化量最终全部转化为焦耳热。

动态变化类：这类题型的显著特点是导体棒的加速度随速度变化，缘由是安培力F_{安}=BIL与速度v成正比（由感应电流I与感应电动势E=BLv相关联），安培力变化会导致合力变化。常见场景包括导体棒从静止开始在磁场中运动（速度增大→安培力增大→加速度减小）、含电容器的电磁感应电路（充电过程中电流变化）。解题需结合动态受力分析（明确F_{å}=ma随v的变化关系）与动量定理（合外力的冲量等于动量变化量I_{å}=Delta p）。

2. 所有题型的共性公式链

无论面对上述哪类题型，均需先通过电磁感应规律求出 “感应电动势→感应电流→安培力”，具体公式及注意事项如下：

感应电动势（切割磁感线场景）：公式为E = BLv，适用条件是磁场B、导体棒长度L、速度v三者两两垂直；若三者不垂直，需取垂直于切割方向的分量代入计算（即E = BLvsin heta， heta为v与垂直于B、L平面方向的夹角）。

感应电流：公式为I = frac{E}{R_{æ»}}，其中R_{æ»}为电路总电阻，等于外电路电阻R_{å}与导体棒自身电阻r之和（即R_{æ»}=R_{å}+r）；若题目未提及导体棒电阻r，则默认r=0，此时R_{总}=R_{å}。

安培力：公式为F_{å®}=BIL，方向需用左手定则判断（磁感线垂直穿掌心，四指指向电流方向，大拇指指向安培力方向），且安培力方向与电流方向、磁场方向均垂直；若B与I不垂直，需取垂直于电流方向的分量（即F_{å®}=BILsinalpha，alpha为B与I的夹角），高中阶段多为垂直场景，故默认sinalpha=1。

二、力电平衡类题型：四步解题法与实战演算

力电平衡类题型的核心逻辑是 “导体棒匀速或匀变速运动时，安培力与其他力的合力为零或恒定”，解题需严格遵循 “定模型→析受力→列方程→解方程” 的四步流程，确保步骤规范、规避易错点。

1. 四步解题流程详解

步骤 1：定模型 —— 明确物理场景关键信息

核心任务是确定导轨类型、磁场方向与导体棒运动状态。具体操作要点包括：①判断导轨类型（水平、斜面或竖直）；②明确磁场方向（是否垂直导轨平面，若不垂直需取垂直于切割方向的分量）；③分析运动状态（匀速运动则F_{合}=0，匀变速运动则F_{合}=ma）。此步骤的常见易错点是忽略磁场与导轨平面不垂直的情况，未对B取垂直分量，导致后续感应电动势计算错误。

步骤 2：析受力 —— 绘制受力图并判断安培力方向

核心任务是完整列出导体棒所受所有力，并准确判断安培力方向。具体操作：①梳理受力种类：重力（mg，方向竖直向下）、支持力（N，方向垂直导轨平面）、拉力（F，若题目存在拉力则需计入）、摩擦力（f=mu N，方向与运动方向相反）、安培力（F_{å®}）；②用左手定则判断安培力方向：让磁感线垂直穿过掌心，四指指向电流方向，大拇指所指方向即为安培力方向。此步骤的易错点是混淆左手定则与右手定则 —— 右手定则用于判断感应电流方向（电磁感应现象），左手定则用于判断安培力方向（磁场对电流的作用力），二者不可混用。

步骤 3：列平衡方程 —— 沿运动方向联立公式

核心任务是沿导体棒运动方向列出合力方程，并与电磁学公式联立。具体操作：①若导体棒匀速运动，沿运动方向列 “合力为零” 的方程（F_{å}=0）；若为匀变速运动，列 “合力等于ma” 的方程（F_{å}=ma）；②将感应电动势E=BLv、感应电流I=frac{E}{R_{总}}、安培力F_{å®}=BIL等电磁学公式代入力学方程，形成方程组。易错点是方程方向符号错误，例如安培力与运动方向相反时，未在方程中取负号，导致受力平衡关系错乱。

步骤 4：解方程 —— 统一单位并计算未知量

核心任务是代入已知数据，求解速度v、拉力F、电阻R等未知量。操作要点：①统一物理量单位（磁场B单位为 T，导体棒长度L为 m，速度v为 m/s，电阻R为 Ω，力F为 N，重力加速度g取9.8m/s²或10m/s²，需按题目要求）；②计算顺序优先求安培力 —— 需先通过E=BLv求感应电动势，再通过I=frac{E}{R_{æ»}}求感应电流，最后代入F_{å®}=BIL计算安培力。常见易错点是单位不统一，例如将磁场单位 Gauss（高斯）直接代入计算，未换算为 T（1T=10⁴Gauss），导致结果偏差。

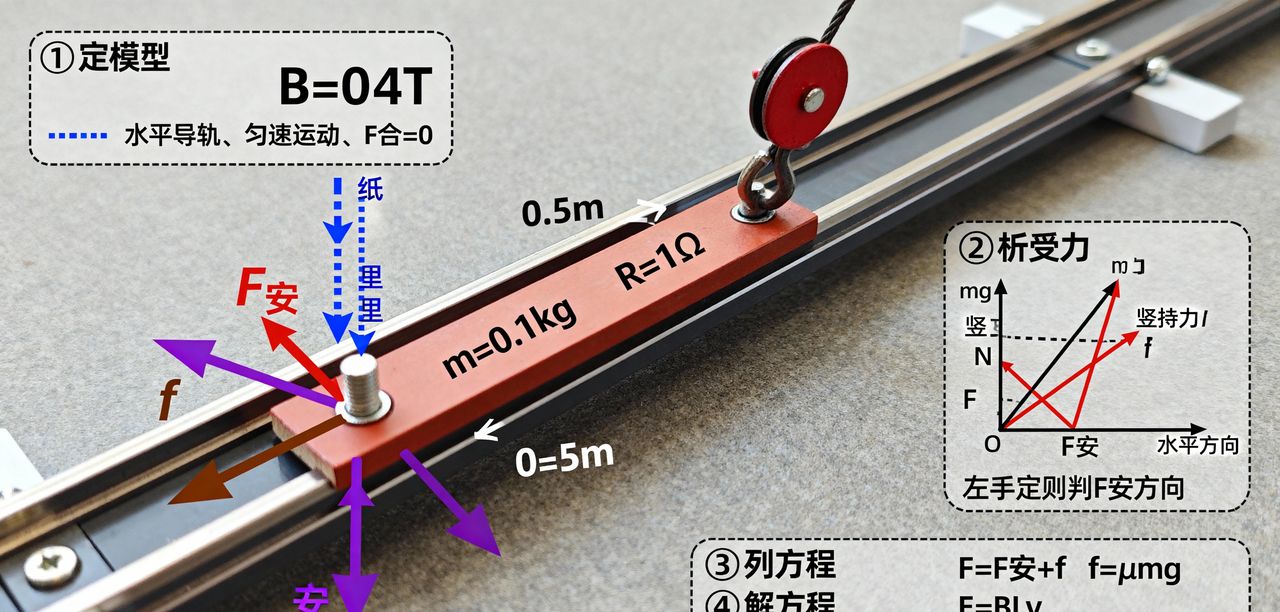
2. 实战实例：水平导轨匀速运动问题

题目：水平导轨间距L=0.5m，匀强磁场B=0.4T垂直纸面向里，导体棒质量m=0.1kg，电阻R=1Ω（不计其他电阻），动摩擦因数mu=0.2，在水平拉力F作用下以v=2m/s匀速运动，求拉力F的大小。

（1）步骤 1：定模型

导轨类型为水平导轨，磁场方向垂直导轨平面向里（B与L、v均垂直，可直接用E=BLv计算感应电动势）；导体棒运动状态为匀速运动，故F_{合}=0；受力分析需包含拉力F（向右，动力）、安培力F_{安}（向左，阻力）、摩擦力f（向左，阻力）。

（2）步骤 2：析受力与安培力方向

竖直方向：重力mg（竖直向下）与支持力N（竖直向上）平衡，故N=mg；

水平方向：拉力F（向右）、安培力F_{安}（向左）、摩擦力f（向左）；

安培力方向判断：先用右手定则判断电流方向 —— 导体棒向右运动切割磁感线，磁感线向里，电流从导体棒左端流向右端；再用左手定则判断安培力方向 —— 磁感线穿掌心（向里），四指指向电流方向（右），大拇指指向左（与运动方向相反）。

（3）步骤 3：列平衡方程与电磁公式

水平方向平衡方程：F = F_{å®} + f；

摩擦力计算：f = mu N = mu mg（因N=mg，水平导轨支持力等于重力）；

电磁公式链计算：

①感应电动势：E = BLv = 0.4×0.5×2 = 0.4V；

②感应电流：I = frac{E}{R} = frac{0.4}{1} = 0.4A（因不计其他电阻，R_{æ»}=R=1Ω）；

③安培力：F_{安} = BIL = 0.4Ã0.4Ã0.5 = 0.08N。

（4）步骤 4：代入数据求解

摩擦力：f = mu mg = 0.2Ã0.1Ã10 = 0.2N（重力加速度g取10m/s²，题目未明确时可合理取值）；

拉力：F = F_{安} + f = 0.08 + 0.2 = 0.28N。

三、能量守恒类题型：三大能量关系与实战案例

能量守恒类题型的核心是 “机械能的减少量等于电能的增加量（最终转化为焦耳热）”，需根据不同物理模型选择对应的能量方程，避免漏项或错项。

1. 三大能量关系（按模型分类）

重力做功关系（适用斜面导轨模型）

当导体棒沿斜面下滑或上滑时，重力势能发生变化，能量方程为mgDelta h = Q + Delta E_{k}（下滑时，Delta h为导体棒下降的高度；上滑时，Delta h为上升高度，此时重力势能增加，方程变为W_{拉} = mgDelta h + Q + Delta E_{k}）。其物理意义是：重力势能的减少量（下滑），一部分转化为电路中的焦耳热Q，另一部分转化为导体棒的动能变化量Delta E_{k}。

拉力做功关系（适用水平导轨受拉力模型）

当水平导轨上的导体棒受拉力运动时，拉力做功提供外部能量，能量方程为W_{F} = Q + Delta E_{k}（若存在摩擦力，需补充摩擦力做功项W_{f}，即W_{F} = W_{f} + Q + Delta E_{k}，W_{f}=mu mgs）。物理意义是：拉力做的功（外界输入的能量），一部分用于克服摩擦力做功（能量损耗），一部分转化为焦耳热Q，另一部分转化为导体棒的动能变化量Delta E_{k}。

安培力做功关系（所有模型通用）

无论何种模型，安培力均为 “阻力”（阻碍导体棒相对磁场运动），安培力做负功，其做功的绝对值等于电路产生的焦耳热，方程为W_{安} = -Q（W_{安}= -F_{安}s，s为导体棒运动距离）。物理意义是：安培力做负功的过程，本质是机械能转化为电能，最终电能全部以焦耳热的形式耗散，因此安培力做功的绝对值与焦耳热相等。

2. 关键说明

焦耳热 的计算：焦耳热有两种计算方式，一是通过能量守恒方程间接求解（适用于变电流场景，如导体棒加速运动时，电流I随速度v变化，无法直接用I²Rt计算）；二是直接用公式Q = I²R_{总}t计算（仅适用于恒定电流场景，需已知电流I、总电阻R_{总}与时间t），且两种方式计算结果需一致（可用于验证）。

动能变化量 ：公式为Delta E_{k} = frac{1}{2}mv_{末}² – frac{1}{2}mv_{å}²，若导体棒做匀速运动（v_{æ«}=v_{å}），则动能变化量Delta E_{k}=0，此时能量方程可简化（如水平导轨匀速运动时，W_{F} = W_{f} + Q）。

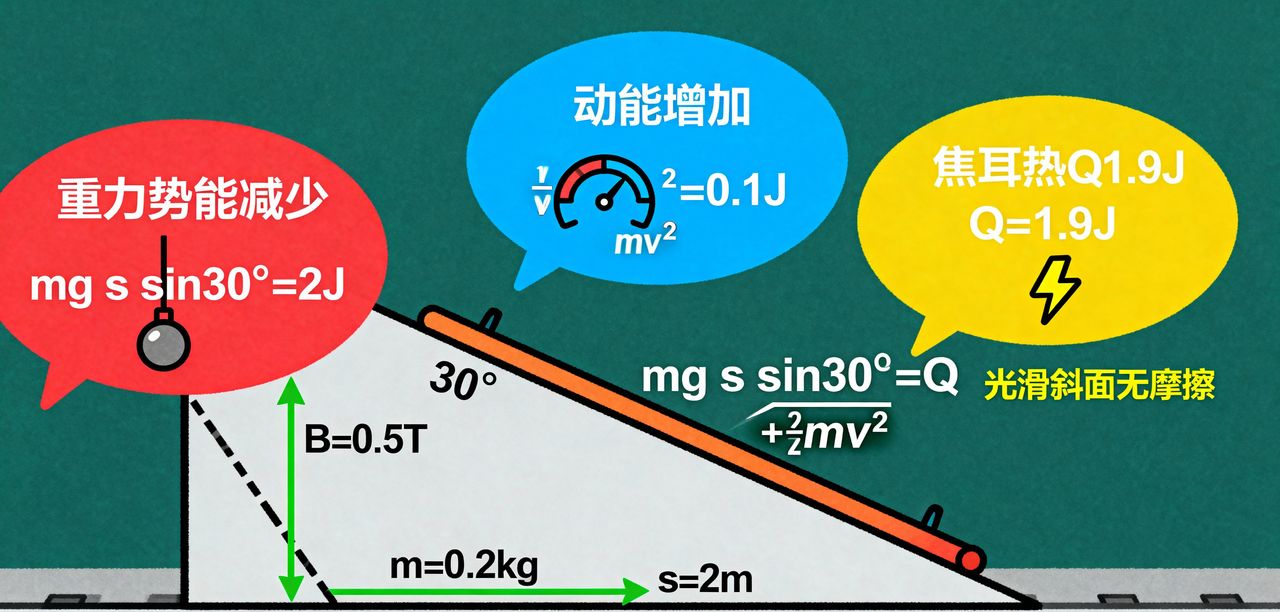
3. 实战案例：斜面导轨下滑模型

题目：导体棒质量m=0.2kg，沿倾角30°的光滑斜面（无摩擦）下滑，导轨间距L=0.4m，匀强磁场B=0.5T垂直斜面向上，电路总电阻R=0.2Ω（含导体棒电阻），下滑距离s=2m，初速度v₀=0，末速度v=1m/s，求电路产生的焦耳热Q。

（1）步骤 1：确定能量转化方向

导体棒沿光滑斜面下滑时，无摩擦力损耗，能量转化关系为：重力势能减少，一部分转化为导体棒的动能（速度从0增至1m/s），另一部分通过安培力做功转化为电路中的焦耳热。因此，能量守恒的核心逻辑是 “重力势能减少量 = 动能增加量 + 焦耳热”。

（2）步骤 2：列能量方程

重力势能减少量：mgDelta h = mg s sin30°（其中Delta h = s sin30°，即下滑距离s对应的竖直高度差，sin30°=0.5）；

动能增加量：Delta E_{k} = frac{1}{2}mv² – frac{1}{2}mv₀²（因初速度v₀=0，简化为Delta E_{k} = frac{1}{2}mv²）；

能量方程：mg s sin30° = Q + frac{1}{2}mv²（无摩擦力，故无摩擦力做功项）。

（3）步骤 3：代入数据求解

已知条件：m=0.2kg，g=10m/s²，s=2m，sin30°=0.5，v=1m/s；

重力势能减少量（方程左边）：mg s sin30° = 0.2Ã10Ã2Ã0.5 = 2J；

动能增加量（方程右边部分）：Delta E_{k} = frac{1}{2}Ã0.2Ã1² = 0.1J；

焦耳热：Q = mg s sin30° – Delta E_{k} = 2 – 0.1 = 1.9J。

四、常见错误：避坑指南（类型 + 分析 + 对策）

电磁感应综合题的高频错误聚焦在 “安培力方向判断”“能量方程漏项”“电路电阻忽略内阻” 三类，需针对性分析错误缘由并制定纠正对策。

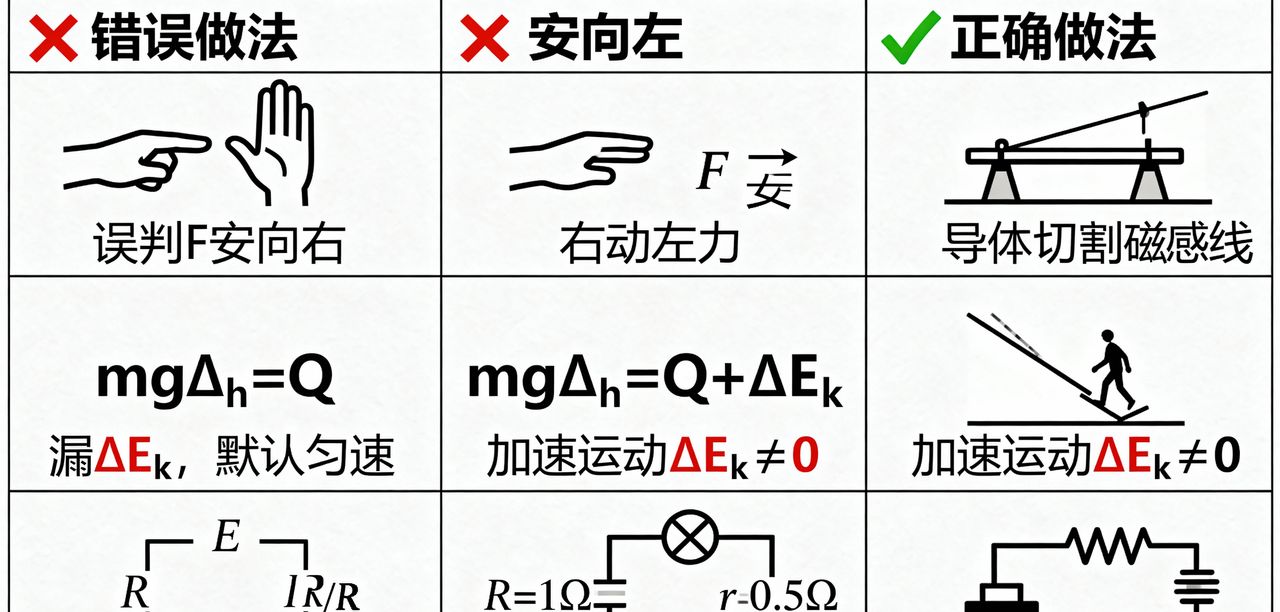
1. 错误 1：安培力方向判断错误（左手 / 右手定则混淆）

错例分析：在水平导轨导体棒向右运动、磁场向里的场景中，误用右手定则判断安培力方向（误判为向右，正确方向应为向左），导致平衡方程错误写为 “F + F_{安} = f”，最终拉力F的计算结果偏小。错误根源是混淆 “感应电流方向判断” 与 “安培力方向判断”—— 右手定则用于判断电磁感应中的电流方向（“因动生电”），左手定则用于判断磁场对电流的作用力（安培力，“因电受力”）。

纠正对策：①牢记 “右动左力” 口诀：判断感应电流方向用右手定则（导体运动→电流），判断安培力方向用左手定则（电流→受力）；②掌握左手定则三步法：第一步，让磁感线垂直穿过掌心（掌心朝向磁场的反方向，如磁场向里则掌心向外）；第二步，四指指向电流方向（与正电荷定向移动方向一致，若为负电荷则相反）；第三步，大拇指所指方向即为安培力方向（安培力与电流、磁场构成 “左手三维直角坐标系”）。

2. 错误 2：能量方程漏写动能变化（默认匀速运动）

错例分析：导体棒加速下滑时，错误将能量方程写为 “mgDelta h = Q”（漏写动能变化量Delta E_{k}），导致焦耳热Q的计算值偏大（实际应为Q=mgDelta h – Delta E_{k}）。错误缘由是未先判断导体棒运动状态 —— 加速运动时动能增加（Delta E_{k}>0），需将 “重力势能减少量” 分配给 “动能” 和 “焦耳热”；仅当导体棒匀速运动时（Delta E_{k}=0），方程才可简化为mgDelta h = Q。

纠正对策：①解题第一步标注导体棒运动状态：通过题目关键词（“匀速”“加速”“从静止开始”）或速度变化（v_{å}与v_{æ«}是否相等）判断；②列能量方程前先计算动能变化量：若v_{æ«}âv_{å}，则Delta E_{k} = frac{1}{2}mv_{æ«}² – frac{1}{2}mv_{å}²，必须列入方程；若题目未明确速度，需通过受力分析判断是否匀速（如合力为零则匀速）。

3. 错误 3：电路电阻忽略导体棒内阻（r）

错例分析：题目明确 “导体棒电阻r=0.5Ω，外电阻R=1Ω”，但计算感应电流时误写为 “I=frac{E}{R}”（正确应为I=frac{E}{R+r}），导致电流I计算值偏大（错误值I=frac{E}{1}，正确值I=frac{E}{1.5}），进而使安培力F_{å®}=BIL偏大。错误根源是默认 “导体棒为理想导体（电阻为零）”，忽略题目中明确给出的导体棒内阻r，违背 “闭合电路欧姆定律（I=frac{E}{R_{æ»}}，R_{æ»}=R_{å¤}+r）”。

纠正对策：①解题前圈画电路电阻信息：若题目提及 “导体棒电阻r”“导线电阻不计”，则R_{æ»}=R_{外}+r；若仅提 “外电阻R”“导体棒电阻不计”，则R_{æ»}=R；②绘制简易电路图：将导体棒视为 “有内阻的电源”（电动势E=BLv，内阻r），外电路为电阻R，直观呈现 “内 + 外” 总电阻，避免遗漏。

五、5 天专项训练计划（目标 + 任务 + 重点 + 方法）

专项训练从 “基础平衡” 到 “综合动态” 逐步升级，每天聚焦 1 类核心题型，通过典型例题巩固解题方法，提升解题速度与正确率，最终实现综合能力突破。

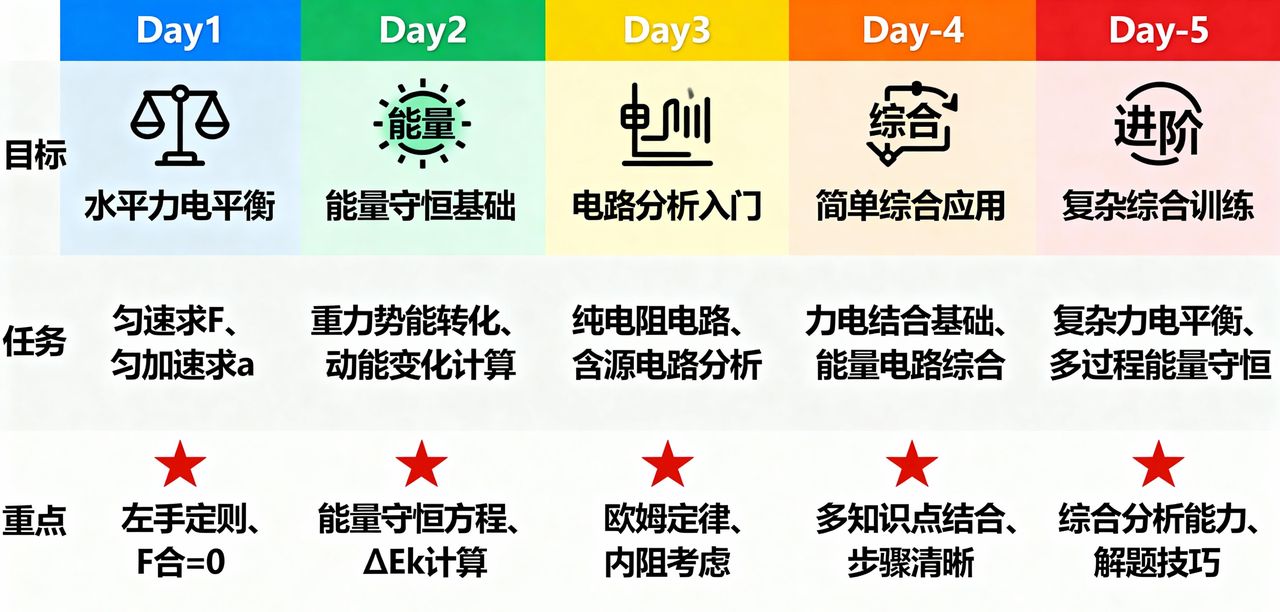
1. Day1：掌握水平导轨力电平衡题型

训练目标：熟练解决水平导轨场景下的力电平衡问题，能准确判断安培力方向、列写平衡方程，正确率达 90% 以上。

具体任务：完成 2 道基础题，分别为 “水平导轨受拉力匀速运动（求拉力F、电路电流I）”“水平导轨受拉力匀加速运动（求加速度a、5s 末速度v）”。

训练重点：安培力方向判断（左手定则应用）、平衡方程列写（匀速时F_{å}=0，匀加速时F_{å}=ma）、单位统一（如 Gauss 换算为 T）。

核心方法应用：左手定则、“感应电动势→感应电流→安培力” 公式链、牛顿第二定律联立。

2. Day2：掌握斜面导轨力电平衡题型

训练目标：攻克斜面导轨力电平衡问题，能准确计算重力分力、分析支持力与摩擦力的关系，解题时间控制在 12 分钟 / 题内。

具体任务：完成 2 道进阶题，分别为 “斜面导轨匀速下滑（求动摩擦因数mu、电路总电阻R_{æ»}）”“斜面导轨匀速上滑（求拉力F、10s 内产生的焦耳热Q）”。

训练重点：重力分力计算（沿斜面mgsin heta、垂直斜面mgcos heta）、支持力与摩擦力关系（f=mu N，N=mgcos heta）、斜面方向平衡方程列写。

核心方法应用：正交分解法（沿斜面、垂直斜面建立坐标系）、力电公式联立求解。

3. Day3：掌握水平导轨能量守恒题型

训练目标：熟练运用能量守恒定律解决水平导轨受拉力的能量问题，能准确计算拉力做功、焦耳热，两种焦耳热计算方法结果一致。

具体任务：完成 2 道基础题，分别为 “水平导轨受恒力F=1N运动（求 5m 内焦耳热Q、末动能Delta E_{k}）”“水平导轨无拉力（仅受摩擦力，求滑行至静止过程中产生的焦耳热Q）”。

训练重点：拉力做功计算（W_{F}=Fscos heta， heta为F与s的夹角，水平场景 heta=0°，cos heta=1）、能量方程列写（W_{F}=Q+Delta E_{k}或Delta E_{k}=Q+W_{f}）。

核心方法应用：能量守恒方程（拉力做功关系）、焦耳热直接计算（Q=I²R_{æ»}t，验证间接求解结果）。

4. Day4：掌握斜面导轨能量守恒题型

训练目标：攻克斜面导轨能量守恒问题，能综合分析重力势能、摩擦力做功与焦耳热的关系，复杂场景（粗糙斜面）解题正确率达 85% 以上。

具体任务：完成 2 道进阶题，分别为 “斜面光滑（求下滑 5m 产生的焦耳热Q、末速度v_{末}）”“斜面粗糙（动摩擦因数mu=0.1，求下滑 5m 产生的焦耳热Q、重力势能变化量）”。

训练重点：重力势能变化计算（mgDelta h=mg ssin heta）、摩擦力做功分析（W_{f}=-mu mgcos heta·s，负号表明阻力做功）、能量方程补充摩擦力项（mgDelta h=Q+W_{f}+Delta E_{k}）。

核心方法应用：多力做功的能量分配分析、能量守恒方程拓展（含重力、摩擦力、安培力做功）。

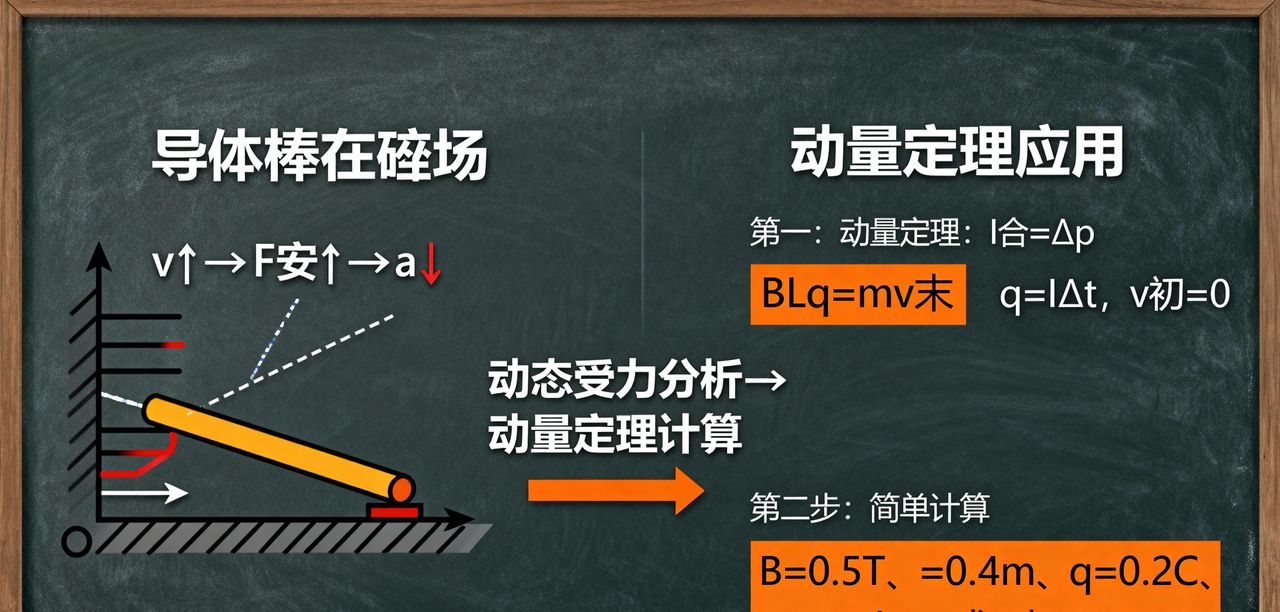
5. Day5：综合应用（含动态变化题型）

训练目标：突破动态变化类综合题，能结合牛顿定律与动量定理分析加速度随速度的变化关系，综合题正确率达 80% 以上。

具体任务：完成 2 道综合题，分别为 “导体棒从静止开始在水平导轨加速（用牛顿定律分析a-v关系，用动量定理求 10s 末速度v）”“含电容器的电磁感应电路（分析充电过程中电流I随时间的变化、电容器最终带电量Q）”。

训练重点：动态受力分析（安培力F_{å‰}=BIL=frac{B²L²v}{R_{æ»}}，随v增大而增大，故F_{å}=F-F_{å®}减小，a=frac{F_{å}}{m}减小）、动量定理应用（合外力冲量I_{å}=Delta p，即Ft – BLq = mv_{æ«} – 0，q=frac{DeltaPhi}{R_{æ»}}=frac{BLs}{R_{æ»}}）。

核心方法应用：牛顿第二定律（动态加速度分析）、动量定理（变力做功场景求速度，规避积分运算）、电容器带电量公式（Q_{容}=CU，U=IR_{外}）。

6. 训练核心目标

通过 5 天专项训练，最终实现三大目标：①力电平衡类题型解题步骤标准化，能在 10 分钟内完成 1 道题；②能量守恒类题型方程列写无漏项，焦耳热Q计算正确率≥90%；③综合题（含动态变化）正确率≥80%，熟练掌握 “电磁公式链与力学 / 能量规律” 的串联方法，形成解题思维闭环。

六、总结

电磁感应综合题的核心是 “电磁规律（法拉第电磁感应定律、左手定则）与力学规律（牛顿第二定律、动量定理）、能量规律（能量守恒定律）的有机结合”，解题的关键在于三点：

一是牢记 “E=BLvâI=frac{E}{R_{æ»}}âF_{å®}=BIL” 的公式链，这是连接电磁学与力学、能量学的核心桥梁，所有题型均围绕此公式链展开，需熟练掌握公式适用条件与单位换算；

二是针对不同题型抓核心逻辑 —— 力电平衡类题型聚焦 “受力分析（正交分解）与合力方程（F_{合}=0或ma）”，通过四步流程规范解题；能量守恒类题型聚焦 “机械能（重力势能、动能）与电能（焦耳热）的转化关系”，根据模型（水平 / 斜面、有无摩擦力）选择对应能量方程，避免漏项；动态变化类题型聚焦 “安培力随速度的变化规律”，结合牛顿定律分析加速度趋势，用动量定理简化计算；

三是主动规避高频错误，通过 “定则区分（右动左力）”“状态判断（匀速 / 加速）”“电路分析（内 + 外电阻）” 等方法，减少 “安培力方向误判”“能量方程漏项”“忽略内阻” 等问题，养成 “先审题标关键、再建模列公式、最后验算查错误” 的解题习惯。

掌握上述方法后，不仅能有效应对期中、期末的电磁感应综合题，更能为后续 “电磁感应与动量结合”“交变电流（感生电动势、动生电动势综合）” 等复杂模块打下坚实基础，逐步建立物理学科的 “跨模块综合思维”，为高三物理复习与高考冲刺做好铺垫。